SLI is an automated theorem prover for first order logic (FOL). SLI is an example of a deductive inference program, capable of proving by refutation using first order logic.

SLI is able to build a graphical representation of a proof. The representation is very close to the proposed in the book 'Artificial Intelligence: A New Synthesis' by Nils J. Nilsson.

As a pedagogic tool for easing the learning of automated theorem proving, SLI includes some features such as:

• Use of FOL as its input language
• Capability of transforming FOL sentences into clauses
• Use of Robinson's Binary Resolution Rule & Factorization Rule
• Proof by refutation principle
• Graphical representation of the proof
• First breadth search implemented
• Maximum depth of search
• and others

Download SLI

SLI should be unziped and it is ready for use.

SLI is really easy to use and its interface is simple.

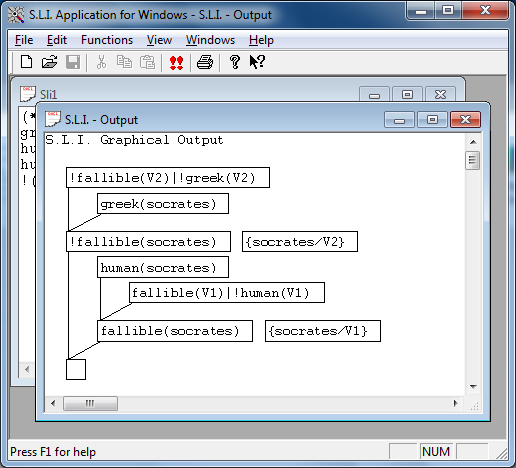
When SLI is able to yield a proof, it is represented as a tree as it appears in the figure below.

The input interface of SLI allows to use just plain characters. The operators have been coded using characters as follows:

Logical operator	SLI coding	Example
And	ampersand (C-language style)	p(X) & q(X)
Or	pipe (C-language style)	p(X) | q(X)
Negation	! (C-language style)	!p(X)
Implication	->	p(X) -> q(X)
Biconditional Implication	<->	p(X) <-> q(X)
Existential quantifier	plus sign	(+X) p(X)
Universal quantifier	Asterisk	(*X) p(X)

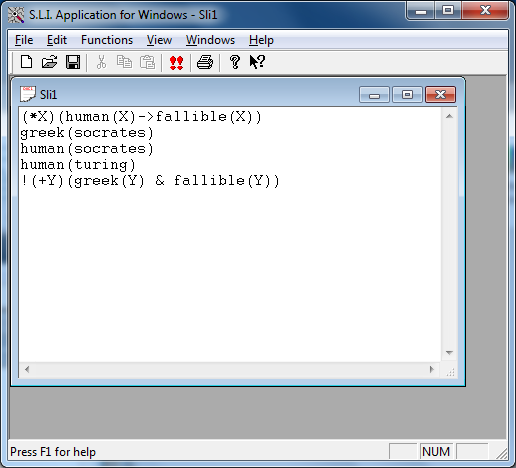
The problem example appearing in the figure above represents the classical 'Fallible Greek' problem. And it can be formulated as follows:

Logic sentence	SLI coding of the logic sentece
Any human is fallible.	(*X)(human(X)->fallible(X))
Socrates is greek.	greek(socrates)
Socrates is human.	human(socrates)
Turing is human.	human(turing)
There exists a fallible greek.	!(+Y)(greek(Y) & fallible(Y))

The last sentence in the list is the theorem we would like to prove.
When using SLI, the theorem to be proved is just added to the set of axioms, negated (the red ! in the last sentence).

Once the problem is coded in the input window, the proof can be obtained

• by pressing Ctrl + E in the keyboard,
• by choosing Functions/Execute in the application menu,
• by clicking with the mouse in the button, in the tool bar.

SLI uses the Robinson's Binary Resolution Principle in order to try to obtain an empty clause from the set of senteces provided by the user.

A requirements when using the Robinson's Binary Resolution Rule is that expressions that can be used should be in a specific format, the clause format.

SLI is able to transform the senteces provided by the user and obtain the equivalent set of clauses.

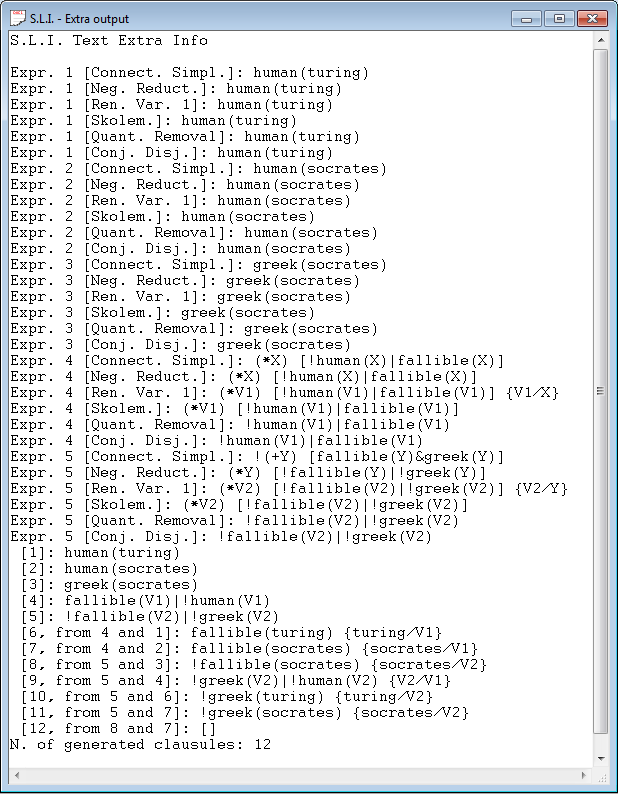
The set of clauses is obtained by a well-known nine steps process. In each step, some standard operations are performed, and the user can watch the result of seven of these operations.

An additional text output can include the result of perform each step for every sentence and, the set of clauses. It also can be obtained the full set of clauses obtained in the process of obtaining the proof.

An example of the textual output is shown in the figure below.

In order to control the amount of information the user want to watch in the textual output, there exists a configuration Window.

The configuration window allows the user to filter the amount of information just by checking options. The configuration windows is shown in the figure below.

SLI relies on a breath-first search algorithm when searching a proof.

The configuration includes a box for establishing the maximum depth factor. This factor is used to calculate the maximum depth when searching together with the number of initial clauses.

If the maximum depth is reached, SLI stops searching and the message "The empty clause cannot be generated" is shown.

In our experience, 3 is a reasonable value for the maximum depth factor.