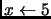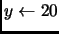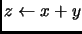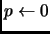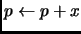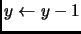Ejercicios de los Temas 1, 2 y 3

 

Versión Postscript

 Version PDF

 

Técnicas de Programación

 

  1. Elaborar un algoritmo que lea una hora expresada en segundos transcurridos desde las 12 de la noche y la convierta en horas, minutos y segundos. Describir el algoritmo en diagrama de flujo y seudocódigo.
  2. Elaborar un algoritmo para determinar si una hora leída en la forma horas, minutos y segundos está correctamente expresada.
  3. Elaborar un algoritmo que lea dos valores y los escriba en orden.
  4. Elaborar un algoritmo para imprimir una tabla de tres columnas y N filas con los cuadrados y los cubos de los N primeros números.
  5. Se quiere repartir caramelos a cuatro niños. Estos caramelos son de tres colores diferentes: rojo, verde y azul, y se encuentran en una bolsa opaca. Con el fin de evitar cualquier disputa, se quiere dar a cada niño el mismo número de caramelos de cada color. Para ello, se preparan tres cajas de colores. Elaborar el algoritmo que resuelva el problema del llenado de las cajas y la distribución de los caramelos.

     

  6. Se definen los números triangulares como los obtenidos de sumar los números naturales sucesivos 1, 2, 3, ...; es decir, los primeros números triangulares son 1, 3, 6, 10, .... Elaborar un algoritmo para imprimir el N-ésimo número triangular. Describir el algoritmo mediante diagrama de flujo y seudocódigo.
  7. Diseñar un algoritmo para imprimir los números impares positivos menores que n.
  8. Deducir los resultados que se obtienen del siguiente algoritmo:

     

    algoritmo ejercicio
    variables x,y,z : entero
    inicio
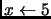
         \(x \leftarrow{} 5\)
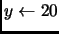
         \(y \leftarrow{} 20\)
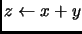
         \(z \leftarrow{} x+y\)
        escribir x,y
        escribir z
    fin

     

  9. Sean x e y dos variables numéricas enteras. El valor inicial de y es superior o igual a 1. Se considera el módulo M cuya descripción es la siguiente :

     

    modulo M
    parametros_entrada x,y : entero
    parametros_salida p : entero
    inicio
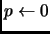
         \(p \leftarrow{} 0\)
        repetir
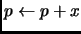
             \(p \leftarrow{} p+x \)
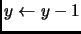
             \(y \leftarrow{} y-1 \)
        hasta_que y=0
    fin

    Describir con palabras lo que calcula el módulo M.

     

  10. (Examen curso 96/97) Escribir en pseudocódigo el algoritmo que resuelva el problema de escribir en pantalla todos los números positivos múltiplos de un valor positivo que se pide por teclado. Nota: Este enunciado se debe interpretar de forma literal.
  11. Supongamos que se debe realizar la agrupación de un documento de 10 páginas que ha sido enviado a un servicio de reprografía. Para cada una de las páginas del documento, el servicio de reprografía ha fotocopiado alrededor de un centenar de ejemplares idénticos, la incertidumbre en el número se debe a que la máquina fotocopiadora funciona defectuosamente. Se han situado 10 mesas, numeradas del 1 al 10, y en cada mesa se encuentra el bloque de fotocopias correspondientes a la página del mismo número. Elaborar un algoritmo para realizar el trabajo, suponiendo que el individuo que ha de realizarlo es capaz de las siguientes funciones:

     

  12. Supongamos que, en un procesador dado, no se pueden calcular restas, pero sí sumas. Tampoco se pueden representar números negativos. Elaborar un algoritmo para calcular M - N , donde M y N son números enteros positivos.
  13. Elaborar un algoritmo para calcular el valor de la siguiente expresión:

     
    N Valor de la expresión
    0 2
    1 8
    2 512

     

  14. Sabiendo que el día 1 de enero de 1.583 fue sábado y que desde entonces no se han producido modificaciones en el calendario, elaborar un algoritmo para calcular el día de la semana en que cayó o caerá una fecha cualquiera posterior al 1 de enero de 1.583. Nota: Un año se considera bisiesto cuando es divisible por 400 o bien es divisible por 4 pero no por 100.
  15. Diseñar un algoritmo que, dados 10 números enteros, indique cuantos de ellos son números pares, nos muestre estos y calcule la media aritmética de los impares.
  16. Diseñar un algoritmo para resolver una ecuación de segundo grado.
  17. Diseñar un algoritmo que calcule el precio de un billete de ida y vuelta por avión, conociendo la distancia a recorrer, el número de días de estancia y sabiendo que si la distancia es superior a 1.000 Km. y el número de días de estancia es superior a 7, la línea aérea le hace un descuento del 30 %. (Precio por kilómetro = 8,50 ptas.).
  18. (Examen curso 86/87) Considérense las tres soluciones al problema "Pelar un número suficiente de patatas que hay en un cesto", teniendo en cuenta que el cesto puede estar vacío en un momento dado.

     

    algoritmo pelar1
    inicio
        mientras número insuficiente de patatas peladas
            si cesto no vacío
                entonces pelar una patata
            fin_si
        fin_mientras
    fin
    algoritmo pelar2
    inicio
        mientras (número insuficiente  de patatas peladas) o (cesto no vacío)
            pelar una patata
        fin_mientras
    fin
    algoritmo pelar3
    inicio
        si cesto no vacío
        entonces
            mientras número insuficiente de patatas peladas
                pelar una patata
            fin_mientras
        si_no comprar una patata
        fin_si
    fin

    ¿Cómo se comportan frente a las siguientes situaciones?:

    ¿Se te ocurre una solución mejor?

Algunos problemas con truco

 

  1. Un pastor con un lobo, una oveja y una paca de hierba tiene que cruzar el río, para lo cual dispone únicamente de una pequeña barca en la que sólo caben el pastor y uno de sus tres acompañantes. ¿Cómo se las arreglará el pastor para llevar a la otra orilla a sus tres acompañantes, teniendo en cuenta que no puede dejar solos ni al lobo con la oveja, ni a la oveja con la paca de hierba?
  2. Una persona va a una fuente con dos cubos de capacidad 4 y 9 litros, respectivamente. ¿Qué deberá hacer para conseguir llevarse 3 litros exactamente?
  3. Describir los pasos necesarios para realizar el siguiente traslado: Un grupo de 34 soldados debe cruzar un río y sólo disponen de un botecito, perteneciente a dos niños. El bote es tan pequeño que únicamente caben los dos niños o sólo un soldado.
  4. Hace poco, asistimos mi esposa y yo a una fiesta en la que había otros 4 matrimonios. Hubo al saludarnos cierto número de apretones de mano. Nadie se dio la mano a sí mismo ni a su cónyuge, ni dio la mano a la misma persona más de una vez. Terminados los saludos, pregunté a cada una de las personas, incluida mi esposa, cuántas manos había estrechado. Las respuestas fueron todas diferentes. ¿Cuántas manos estrecho mi mujer?
  5. Determinar la veracidad o falsedad de los cinco enunciados siguientes:

     

    1. Exactamente uno de los enunciados de esta lista es falso.
    2. Exactamente dos de los enunciados de esta lista son falsos.
    3. Exactamente tres de los enunciados de esta lista son falsos.
    4. Exactamente cuatro de los enunciados de esta lista son falsos.
    5. Exactamente cinco de los enunciados de esta lista son falsos.