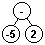Traducción de una expresión en un arbol binario
En esta página se describen algunos algoritmos que permiten obtener
la representación en arbol binario de una expresión matemática
partiendo de la lista de términos que la componen expresados en la notación
habitual (notación infija).
El tipo de expresiones que pueden traducir estos algoritmos está limitado
a las condiciones expuestas en la práctica del curso 00/01,
en el último apartado se exponen algunas técnicas para que puedan tratar
expresiones más complejas.
1. Introducción
Para nuestro problema una expresión matemática será un medio
que permite indicar el orden en que se deben realizar una serie de operaciones para obtener un
resultado. Las operaciones se indican mediante operadores, que en nuestro caso representan
las operaciones suma, resta, producto, división e igualdad, todas ellas operaciones
binarias (necesitan exactamente dos argumentos para poderse evaluar).
Existen varias notaciones para representar expresiones matemáticas, que se
diferencian en el orden en que se escriben los argumentos (operandos) de los operadores.
Las más relevantes son:
- Notación infija: La notación habitual. El orden es primer operando,
operador, segundo operando.
- Notación prefija: El orden es operador, primer operando, segundo operando.
- Notación postfija: El orden es primer operando, segundo operando, operador.
- Notación funcional: Se escribe el operador/función y despues, entre
paréntesis, los operadores separados por comas.
La notación infija tiene el problema de que en expresiones con más de un
operador existe ambiguedad sobre cual es el orden de evaluación. Por ejemplo, la
expresión 8/4/2 se puede interpretar como (8/4)/2 o bien como 8/(4/2). Las otras notaciones
no sufren este problema.
Para resolver estas ambiguedades, se añaden unas reglas denominadas orden de precedencia
de operadores. Cuando dos operadores compiten por el mismo operando (en el ejemplo anterior, el
primer y el segundo operador de división se disputan el operando 4) gana el
el operador (se evalúa primero) con mayor precedencia, o a igualdad de precedencia,
el operador situado más a la izquierda.
Las reglas de precedencia habituales son que los operadores división y producto tienen
igual precedencia y ganan al resto de operadores, y que los operadores suma y resta tienen
igual precedencia y ganan al operador igualdad.
Así, la expresión 8/4/2 se evalúa como (8/4)/2, y 2+3*4 se evalúa como
2+(3*4). Si deseamos cambiar el orden de evaluación, se pueden agrupar partes de una expresión
utilizando paréntesis. En el resto de las notaciones no es necesario utilizar paréntesis ya
que siempre podemos indicar el orden exacto de evaluación sin que exista ambiguedad.
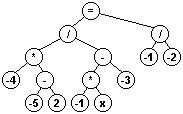
Por ejemplo, si deseamos representar las expresiones (2+(3*4)) = x y ((2+3)*4)= x en
las cuatro notaciones mencionadas, el resultado sería:
| |
(2+(3*4)) = x | ((2+3)*4) = x |
| Notación prefija |
= + 2 * 3 4 x |
= * + 2 3 4 x |
| Notación infija |
2+3*4 = x |
(2+3)*4 = x |
| Notación postfija |
2 3 4 * + x = |
2 3 + 4 * x = |
| Notación funcional |
igual(suma(2,producto(3,4)),x) |
igual(producto(suma(2,3),4),x) |
Generalmente a la hora de traducir una expresión en notación infija a su representación
como arbol binario se suele efectuar un primer paso de traducción a una notación más
adecuada (generalmente a notación prefija o postfija), y luego se traduce la expresión en esa
notación a arbol binario.
Las dos etapas anteriores se pueden realizar directamente mediante un algoritmo recursivo, o en dos pasos
utilizando estructuras adicionales (generalmente pilas).
2. Algoritmo recursivo
Es posible traducir directamente una expresión en notación infija a un arbol binario
mediante uno o varios subprogramas recursivos, aunque el algoritmo no es trivial. En lugar de intentar
desarrollar un único subprograma que analize completamente una expresión, suele ser
más sencillo utilizar un enfoque ligeramente distinto, utilizando dos subprogramas:
-
El primero de ellos se encargaría de asignar el operando derecho a un operador, el cual
se proporciona como un arbol binario al que le falta el hijo derecho, utilizando para ello la lista
de términos correspondiente a la parte de la expresión que falta por traducir. El resultado del
subprograma será el arbol binario completado y la lista de términos que faltan por
analizar.
- El segundo subprograma traduce parte o toda una expresión en un arbol binario, que pasa a
considerarse como operando. Una expresión en notación infija responde al esquema N1 O1
N2 O2 N3..., donde los términos Ni son
operandos y los términos Oi operadores. Este subprograma construiríia
el arbol binario asignando N1 como operando izquierdo de O1, y llamaría
al subprograma anterior para encontrar el operando derecho de O1. Por ejemplo,
en la expresión 2*3+4, el operando derecho del producto es 3, pero en la expresión
2+3*4 el operando derecho de la suma es el arbol binario (3*4).
- Si en algun momento aparece un paréntesis izquierdo en lugar de un operando, se llamaría
al segundo subprograma para que traduzca esa subexpresión al arbol binario correspondiente, que
pasa a considerarse como el operando que faltaba.
3. Conversion de notacion infija a postfija
El siguiente algoritmo en pseudocódigo traduce una expresión en notación infija a
notación postfija, como paso previo a la obtención del arbol binario correspondiente a la
expresión:
- Entrada: Una lista que contiene los terminos de la
ecuacion en notación infija (la notación habitual).
- Salida: Una lista que contiene los terminos de la
ecuacion en notacion postfija.
- Datos locales: Una pila, que va a contener operadores y
parentesis izquierdos.
INICIO
Crear pila y la lista de salida, inicialmente vacias.
MIENTRAS lista de entrada no este vacia y
no se ha encontrado ningun error HACER
Extraer el primer termino de la lista (lo llamaremos E)
SEGUN-SEA E
CASO E es número :
Insertar E al final de la lista de salida
CASO E es la variable x :
Insertar E al final de la lista de salida
CASO E es un paréntesis izquierdo :
Insertar E en la pila
CASO E es un paréntesis derecho :
MIENTRAS La pila no este vacía y
su cima no sea un paréntesis izquierdo HACER
Extraer elemento de la pila
Insertarlo al final de la lista de salida
FIN-MIENTRAS
SI Encontramos el parentesis izquierdo ENTONCES
Extraerlo de la pila y destruirlo
SINO
Se ha detectado un ERROR 2
FIN-SI
Destruir E
CASO E es un operador :
MIENTRAS La pila no este vacía y
su cima sea un operador
de precedencia mayor o igual que la de E HACER
Extraer elemento de la pila
Insertarlo al final de la lista de salida
FIN-MIENTRAS
Insertar E en la pila
FIN-SEGUN-SEA
FIN-MIENTRAS
MIENTRAS Pila no esté vacía HACER
Extraer elemento de la pila
Insertarlo al final de la lista de salida
FIN-MIENTRAS
Destruir pila
FIN
A continuación se muestra el estado de la lista de entrada, la lista de salida y
la pila en cada iteración del bucle principal del algoritmo al dar como entrada la
lista de términos correspondiente al ejemplo del enunciado de la práctica. En color
rojo se muestra el término que se procesa en cada iteración, y en color verde los
términos que se han aņadido a la lista de salida o a la pila como consecuencia de las
acciones realizadas en la iteración anterior:
| -4 | * | ( |
-5 | - | 2 |
) | / | ( |
-1 | * | x |
- | -3 | ) |
= | -1 | / |
-2 |
| * | ( |
-5 | - | 2 |
) | / | ( |
-1 | * | x |
- | -3 | ) |
= | -1 | / |
-2 |
|
| | |
|
| | |
|
| ( |
-5 | - | 2 |
) | / | ( |
-1 | * | x |
- | -3 | ) |
= | -1 | / |
-2 |
|
| | |
|
| | |
|
| -5 | - | 2 |
) | / | ( |
-1 | * | x |
- | -3 | ) |
= | -1 | / |
-2 |
|
| | |
|
| | |
|
Nota: El algoritmo anterior no puede detectar errores
relacionados con la ausencia de paréntesis de cierre.
Aunque con una pequeña modificación es posible
detectarlos, se ha preferido hacerlo en la siguiente etapa:
4. Traducción de notación postfija a arbol binario
- Entrada: La lista obtenida en el algoritmo anterior,
que contiene los terminos de la ecuacion en notación postfija.
- Salida: Un arbol binario que representa la ecuación.
- Datos locales: Una pila, que va a contener operandos (numeros, la
variable x y expresiones (subarboles).
INICIO
Crear pila y arbol, inicialmente vacios.
MIENTRAS lista de entrada no este vacia y
no se ha encontrado ningun error HACER
Extraer el primer termino de la lista (lo llamaremos E)
SEGUN-SEA E
CASO E es número :
Insertar E en la pila
CASO E es la variable x :
Insertar E en la pila
CASO E es una expresión (un arbol) :
Insertar E en la pila
CASO E es un paréntesis izquierdo :
Se ha detectado un ERROR 2
CASO E es un operador :
SI La pila tiene menos de dos elementos ENTONCES
Se ha detectado un ERROR 3
SINO
Extraer elemento de la pila (lo llamaremos A2)
Extraer elemento de la pila (lo llamaremos A1)
Crear un arbol donde la raiz contenga al operador E,
el hijo izquierdo sea A1 y el hijo derecho sea A2
Insertar el arbol en la pila
FIN-SI
FIN-SEGUN-SEA
FIN-MIENTRAS
SI pila vacía o con más de un elemento ENTONCES
Se ha detectado un ERROR 3
SINO
Extraer elemento de la pila (lo llamaremos E)
SI Elemento no es una expresión (un arbol) ENTONCES
Convertir E en un arbol con hijo izquierdo y derecho vacíos
FIN-SI
El resultado del algoritmo (el arbol de salida) es E
FIN-SI
{ Borrado de la pila, si se ha producido error }
MIENTRAS pila no esté vacía HACER
Extraer elemento de la pila
Destruir elemento
FIN-MIENTRAS
Destruir pila
FIN
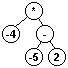
A continuación se muestra el estado de la lista de entrada y la pila al ejecutar el
algoritmo anterior sobre la lista de terminos en notación postfija obtenidos anteriormente.
Para abreviar el listado, cuando varios términos consecutivos de la lista son operandos se han
agrupado las iteraciones correspondientes en una única linea:
|
|
| | |
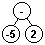 |
-4 |
|
|
|
| | |
| x |
-1 |
 |
|
|
|
| | |
| -3 |
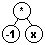 |
 |
|
|
|
| | |
| -2 |
-1 |
 |
|
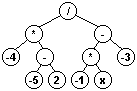
El resultado es el arbol binario resultante de extraer el único termino existente en
la pila.
5. Traducción de expresiones más complejas
Aunque no es necesario para la realización de la práctica, se ha incluido este apartado
para aquellos que deseen saber cómo ampliar los algoritmos anteriores para el tratamiento de
expresiones más complejas, que incluyan variables, excepciones a la regla de precedencia,
operadores unarios y funciones.
- Variables: En los ejemplos anteriores sólo estaba permitido utilizar una variable,
denominada x. Si se desea utilizar cualquier número de variables con otros nombres, lo
único que se necesita es adaptar la definición del término de tipo variable para
que almacene una cadena de caracteres correspondiente a su nombre. No es necesario cambiar ninguno de
los algoritmos anteriores.
- Excepciones a las reglas de precedencia: Los operadores potencia y asignación presentan
excepciones a la regla de precedencia. Cuando el operador potencia compite con otro operador potencia por
un operando, gana el operador situado más a la derecha en la expresión, al contrario
de lo habitual. Por ejemplo, la expresión 2^3^4 se interpreta como 2^(3^4).
El operador asignación (Nota: Nos referimos al operador matemático, no al operador
de Pascal) tiene definida la mayor precedencia posible respecto a los operandos que estén a su
izquierda, y la menor precedencia posible respecto a los que estén a su derecha. Por ejemplo, la
expresión a+b <- c+d se interpreta como a+(b <- (c+d)).
Para tratar estos casos lo más sencillo es definir, para cada operador, dos valores de precedencia:
La precedencia izquierda (que se aplica a los operandos situados a la izquierda del operador) y la
precedencia derecha (que se aplica a los operandos situados a la derecha). Al comparar la precedencia de
dos operadores, se debe escoger los valores de precedencia izquierda o derecha para cada uno de ellos
dependiendo de como estén situados respecto al operando.
- Operadores unarios: Los operadores unarios (negación, factorial, etc.) se suelen
tratar usando los valores de precedencia derecha e izquierda definidos en el punto anterior. Para ello,
se da un valor negativo a la precedencia que corresponda a un operando que, por su posicion respecto
del operador unario, no pueda ser argumento suyo. Por ejemplo, el operador negacion no se aplica sobre
operandos situados a su izquierda, ni el operador factorial sobre operandos situados a su derecha.
Los algoritmos anteriores se deben cambiar de forma que cuando un operador unario reciba un operando
se considere completo (y por lo tanto pase a considerarse un operando). Cualquier disputa entre
operadores sobre un operando se trata de la manera habitual, ya que los valores de precedencia asignados
garantizan la correcta asignación de operandos a operadores.
- Funciones: Las funciones se representan mediante un nombre al que le sigue un número
variable de argumentos separados por comas y encerrados entre paréntesis. En principio parece
que no es posible traducir directamente funciones con los algoritmos anteriores, ni representarlas
adecuadamente mediante árboles binarios, ya que pueden tener más de dos argumentos.
Sin embargo, si hacemos que el símbolo coma represente el operador binario lista de
argumentos y representamos las funciones como operadores unarios que se aplican al operando
derecho, los algoritmos anteriores pueden representar funciones sin necesidad de ninguna modificación.