Programacion II (Sistemas) - Problemas del curso 2002/03

I.T.I. Sistemas - Programación II

Problemas de la asignatura, curso 2002/03

Atención: Si teneis problemas al visualizar ésta página o las soluciones de los problemas, hacermelo saber enviandome un correo a la dirección cvaca@infor.uva.es.

En los días que faltan hasta el examen ire añadiendo nuevas soluciones. Podeis solicitar la resolución de un problema concreto utizando el siguiente formulario (o por e-mail):

1. Clasificar los módulos siguientes de acuerdo a su cohesión:

Un módulo que calcula la mediana de un vector y además devuelve el vector ordenado (la ordenación del vector se aprovecha para calcular la mediana).
Un módulo que recibe un vector y un valor entero t. Dependiendo de lo que valga t el módulo devuelve el valor mínimo o bien el valor máximo o bien la media del vector.
Un módulo recibe dos valores de tipo real, a y b, y un valor entero t. Dependiendo de lo que valga t el módulo devuelve a^b o bien 1/a o bien log_a(b).
Un módulo que recibe dos valores enteros a y b que representan la fracción a/b y devuelve los valores c y d que representan la fracción simplificada c/d cuyo valor es igual a a/b pero donde se han eliminado los factores comunes al numerador y denominador. Para llevar a cabo la simplificación el módulo llama a otro que calcula el máximo común denominador de a y b.

2. Desarrollar baterías de prueba mediante los métodos de caja blanca y caja negra para la siguiente función (errónea), cuyo objetivo es calcular el mínimo de dos valores:

function min(a,b: integer): integer;

Post: { (a < b

min = a), (a ≥ b

min = b) }

begin

if a < b then min := a else if a > b then min := b

end;

3. Se dispone de una función cuyo objetivo es resolver una ecuación del tipo a·x²+b·x+c = 0. La función recibe como parámetros los valores reales a, b, c y devuelve las soluciones de la ecuación, x₁ y x₂, y el valor entero tipo con el siguiente significado:

tipo = 4 significa que la ecuación no depende de x (a y b son nulos) y c es igual a cero. En éste caso y el siguiente x₁ y x₂ no almacenan valores válidos.
tipo = 3 significa que la ecuación no depende de x (a y b son nulos) y c es distinto de cero.
tipo = 2 significa que la ecuación tiene una única solución, ya sea porque el discriminante es nulo o porque a es nulo. En este caso x₂ no almacena un valor válido.
tipo = 1 significa que la ecuación tiene soluciones complejas (x₁ y x₂ no almacenan valores válidos).
tipo = 0 significa que la ecuación tiene dos soluciones reales distintas.

Escribir la postcondición de la función y elaborar baterías de pruebas mediante los métodos de caja negra y caja blanca (en éste último caso primero se debe escribir el código de la función).

4. Se dispone de una función cuyo objetivo es clasificar un triángulo como equilátero (los tres lados iguales), isósceles (dos lados iguales, uno distinto) o escaleno (los tres lados distintos). La función recibe como parámetro las longitudes (números enteros) de los tres lados del triángulo, y se establece como precondición que estas longitudes deben ser positivas no nulas.

En el caso de que no se pueda formar un triángulo con esas longitudes, porque una de ellas sea mayor que la suma de las otras dos se devolverá el valor error.

Escribir la precondición y postcondición de la función.
Elaborar una batería de pruebas mediante el método de caja negra.
Escribir una función que resuelva el problema y en base al código obtenido elaborar una batería de pruebas mediante el método de caja blanca.

5. Se dispone de una función cuyo objetivo es clasificar como agudo, recto u obtuso el ángulo que forma una determinada línea con el eje horizontal. La línea se define como aquella que pasa por el origen de coordenadas y por un punto del semiplano superior. Las coordenadas de este punto son los valores que recibe la función como parámetro. Ejemplo:

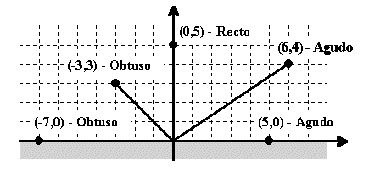
Si el punto no cumple los siguientes requisitos, se devolverá el valor error:

Debe pertenecer al semiplano superior o al eje horizontal.
No puede ser el origen de coordenadas (existirían infinitas líneas posibles).

Escribir una postcondición para ésta función y elaborar una batería de pruebas por el método de caja negra.

6. Se dispone de un módulo, rectangulo, que recibe como entrada cuatro valores enteros, x₀, y₀, x₁ e y₁, que representan las coordenadas del vértice superior izquierda (x₀, y₀) y del vértice inferior derecho (x₁, y₁) que definen a un rectángulo, y que se encarga de detectar los casos especiales en que estas coordenadas corresponden a una línea horizontal (y₀ = y₁), línea vertical (x₀ = x₁), o a un punto (x₀ = x₁ e y₀ = y₁).

El módulo proporciona como salida un valor entero con el siguiente significado: 0 - punto, 1 - línea horizontal, 2 - línea vertical, 3 - rectángulo.

Obtener la batería de pruebas resultante de aplicar el método de caja negra al módulo anterior. Como precondición se exige que las coordenadas de los vértices cumplan que x₀ ≤ x₁, y₀ ≤ y₁.

7. Elaborar una batería de pruebas para un módulo que recibe como entrada una cadena de caracteres y determina si puede ser una clave válida o no (por lo tanto devuelve un valor lógico, cierto o falso). Una clave se considera válida si cumple los requisitos siguientes:

Esta formada por más de 4 y menos de 8 caracteres.
Los caracteres permitidos son las letras a..z, A..Z, los dígitos 0..9 y el carácter %.
Contiene al menos dos letras.
Contiene al menos un carácter que no es letra.
El primer y último carácter son letras.

8. Se dispone de un módulo que recibe como entrada dos parámetros enteros, a y b. El objetivo del módulo es determinar si b divide exactamente a a. Las salidas posibles del módulo son:

IGUALES: Si ambos valores son iguales.
CONGRUENTE: Si b divide exactamente a a y ambos valores no son iguales.
INCONGRUENTE: Si b no divide exactamente a a.
ERROR: Se considera como errónea una entrada en la que b sea nulo.

Diseñar un conjunto de casos de prueba para el módulo anterior mediante el método de pruebas de caja negra.

9. Crear una batería de pruebas mediante el método de caja blanca para el siguiente módulo:

procedure f(a,b: integer; var x: integer);

begin

if (a > 1) and (b = 2) then x := x div a;

if (a = 2) or (x > 1) then x := x+1

end;

10. Compruebe la corrección de los siguientes fragmentos de código:

{ n = 1 } n := m; { m > -10 }
{ z = x²+1, y = 2x } x := x+1; { z + y = x² }
{ x = 10 } x := 2; { x = 2 }
{ } if x < 0 then x := -x; { x ≥ 0 }

11. Determine las postcondiciones más fuertes que garantizan los siguientes fragmentos de código (ver la nota del siguiente problema):

{ x > 10 } y := z; { ... }
{ x > 10 } z := x*(x+1); { ... }
{ b = x } a := b div 3; a := a*3; { ... }
{ x > 5, y < 5 } if (x<0) or (y<0) then x := x*y else y := x*y; { ... }

12. Determine las precondiciones más débiles que hacen correctas los siguientes fragmentos de código: (las variables n y m son de tipo entero, a y b son enteros no negativos, x e y son de tipo real y c de tipo boolean).

Nota: En aquellas expresiones en las que intervengan los operadores cociente (div) y resto (mod) se pueden aplicar las reglas siguientes:

{ a ≥ 0, b > 0, q = a div b, r = a mod b } { a = q·b+r, 0 ≤ r < b, 0 ≤ q < a }
{ a ≥ 0, b > 0, q = a div b } { 0 ≤ q < a, α : 0 ≤ α < b : a = q·b+α }
{ a ≥ 0, b > 0, r = a mod b } { 0 ≤ r < b, a : 0 ≤ α < a : a = α·b+r }

{ ... } n := m; { n ≤ 100 }
{ ... } n := 2*n; { n ≤ 100 }
{ ... } n := n+1; { n = n+1 }
{ ... } c := c or (n=0); { c = false }
{ ... } y := sqrt(x); { y < 2 }
{ ... } a := 10 mod b; { a > 5 }
{ ... } a := b div 10; { a ≥ 0 }
{ ... } if x < 0 then x := -x; { x < 0 }

13. Verificar la siguiente función, estableciendo su precondición y postcondición:

function int(x0,y0: integer) dev x1,y1: integer;

begin

<x1,y1> := <x0,y0>;

x1 := x1+y1;

y1 := x1-y1;

x1 := x1-y1

end

14. Verificar la siguiente función e indicar, examinando la postcondición obtenida en la función ordena2, si ésta función cumple su objetivo de devolver sus dos parámetros en orden de menor a mayor.

function min(a,b: integer) dev m: integer;

begin

if a < b then m := a else m := b

end;

function max(a,b: integer) dev m: integer;

begin

if a > b then m := a else m := b

end;

function ordena2(x0,y0: integer) dev x1,y1: integer;

begin

<x1,y1> := <x0,y0>;

x1 := min(x1,y1);

y1 := max(x1,y1)

end;

15. Verifique la función ordena3 y cree una batería de pruebas por el método de caja negra basada en la postcondición que haya obtenido.

function intercambia(a,b: integer) dev c,d: integer;

begin

c := b; d := a;

end;

function ordena3(x0,y0,z0: integer) dev x1,y1,z1: integer;

begin

<x1,y1,z1> := <x0,y0,z0>;

if x1 > y1 then <x1,y1> := intercambia(x1,y1);

if x1 > z1 then <x1,z1> := intercambia(x1,z1);

if y1 > z1 then <y1,z1> := intercambia(y1,z1);

end;

16. Realizar verificación inversa sobre la siguiente función, encontrando la precondición que garantiza el cumplimiento de la postcondición:

function ordena3(x0,y0,z0: integer) dev x1,y1,z1: integer;

begin

{ ¿? }

<x1,y1,z1> := <x0,y0,z0>;

if x1 > y1 then <x1,y1> := <y1,x1>;

if x1 > z1 then <x1,z1> := <z1,x1>;

if y1 > z1 then <y1,z1> := <z1,y1>;

{ x₁ < y₁ < z₁ }

end;

17. Verificar la corrección total de las siguientes funciones:

function A(x,y: integer) dev z: integer;

var r: integer;

begin

r := 0; z := x;

while r <> y do

begin

z := z+1;

r := r+1

end

end;

function B(x,y: integer) dev z: integer;

var r: integer;

begin

r := 0; z := x;

while z < y do

begin

z := z+1;

r := r+1

end

end;

18. Verificar la corrección total de la siguiente función:

function potencia(a: real; b: integer) dev p: real;

var i: integer;

begin

{ b ≥ 0 }

<p,i> := <1,b>;

while i > 0 do <p,i> := <p*a,i-1>

end;

19. Dada la siguiente función, verificar la corrección parcial de la misma y establecer la condición inicial que debe cumplir u para que se verifique la corrección total:

function fact(u: integer) dev f: integer;

var k: integer;

begin

{ ¿? }

<f,k> := <1,0>;

while k <> u do

begin

k := k+1;

f := f*k

end

{ f = u! =

α : 1 ≤ α ≤ u : α }

end;

20. Verificar la corrección parcial de la siguiente función cuyo objetivo es calcular el n-ésimo término de la sucesión de Fibonacci (F_n), teniendo en cuenta que ésta sucesión se define de la siguiente forma:

F₀ = 0, F₁ = 1
F_n = F_n-1 + F_n-2

function Fib(n: integer) dev x: integer;

var x0,t,i : integer;

begin

{ n ≥ 0 }

<x0,x> := <0,1>;

for i := 1 to n do

begin

t := x0+x;

x0 := x;

x := t

end

{ x = F_n }

end

21. Dada la siguiente función, cuyo objetivo es calcular el máximo común divisor mediante el algoritmo de Euclides.

Crear una batería de pruebas usando el método de caja blanca.
Verificar la corrección total de la siguiente función teniendo en cuenta que:

mcd(u,u) = u
mcd(u,v) = mcd(v,u)
u > v mcd(u,v) = mcd(u - v, v)

function MCD(x,y: integer) dev m: integer;

var

a,b: integer;

begin

{ x > 0, y > 0 }

a := x; b := y;

while a <> b do

if a > b then a := a-b else b := b-a;

m := a

{ m = mcd(x,y) }

end;

22. Se dispone de las siguientes funciones cuyo objetivo es comprobar si un número es primo o no:

function primo1(n: integer): boolean;

var d: integer;

begin

d := n-1;

while (n mod d <> 0) and (d > 2) do

begin

d := d-1

end;

primo1 := n mod d <> 0

end

function primo2(n: integer): boolean;

var d: integer;

begin

d := n-1;

while not((n mod d = 0) or (d > 2)) do

begin

d := d-1

end;

primo2 := n mod d <> 0

end

Sabiendo que una función que compruebe que un número es primo debe tener como precondición que n sea mayor que cero y como postcondición la siguiente expresión:

{ n ≤ 2

primo = true,

( n > 2 ,

α : 2 ≤ α < n :

β : β > 0 : n = α·β )

primo = false,

( n > 2 , ¬ (

α : 2 ≤ α < n :

β : β > 0 : n = α·β) )

primo = true }

Crear una batería por el método de caja negra para las funciones anteriores.
Crear una batería por el método de caja blanca para cada una de las funciones anteriores.
Obtener mediante verificación la postcondición de cada una de las funciones anteriores y comprobar si coincide o no con la postcondición correcta.
Escribir en Eiffel una función que compruebe si un número es primo o no incluyendo la precondición, postcondición, invariante y variante del bucle.

23. Se dispone de la siguiente función, cuyo propósito es calcular una aproximación a la raíz cuadrada del valor x que cumpla que su distancia al valor real de la raíz sea menor que la cota e (ver la postcondición).

function raiz(x,e: real) dev r: real;

var a,b,m,d: real;

begin

{ x ≥ 0, .. }

<a,b> := <0,x>;

d := b-a;

while d > e do

begin

m := (a+b)/2.0;

if m*m > x then b := m else a := m;

d := b-a

end;

r := a

{ |r - √x| ≤ e }

end;

Demostrar la corrección parcial de la función. Al buscar candidatos a invariante del bucle puede ayudar el comprobar si la expresión a ≤ √x ≤ b podría o no formar parte de él.
Demostrar la corrección total de la función e indicar, si se da el caso, las modificaciones que se deben realizar a la precondición para poder garantizar la finitud.

24. Verificar la corrección parcial y total de la siguiente función indicando qué hace:

function f(x,y: integer) dev p: integer;

var t,s: integer;

begin

{ x > 0, y > 0 }

<p,s> := <0,x>;

while x <> 0 do

begin

t := 0;

while t < y do <p,t> := <p+1,t+1>;

x := x-1;

end

end;

25. Se dispone de la siguiente función:

function incognita(x,y: integer) dev z: integer;

var a,b: integer;

begin

if x < y then <a,b> := <x,y> else <a,b> := <y,x>;

while a <> b do

begin

a := a+1;

b := b-1

end;

z := a

end;

Realizar la corrección parcial, obteniendo la postcondición. ¿Qué es lo que calcula la función?
Comprobar la finitud del bucle. Si no se pudiera demostrar, indicar cual sería la condición que se debería añadir al invariante del bucle para garantizar la finitud, y, consecuentemente, la precondición que es necesario imponer a la función.

26. Verificar la corrección total de la siguiente función y crear una batería de pruebas de caja blanca.

function prod(a,b: integer) dev z: integer;

var x,y : integer

begin

{ a > 0 }

<x,y,z> := <a,b,0>;

while x <> 0 do

begin

if impar(x) then z := z+y;

<x,y> := <x div 2,y := 2*y>

end

end;

27. Verificar la corrección total de la siguiente función:

function prod(a,b: integer) dev z: integer;

var x,y: integer;

begin

{ a > 0 }

<x,y,z> := <a,b,0>;

while x <> 0 do

begin

z := z+y*(z mod 10);

<x,y> := <x div 10,10*y>

end

end;

28. Verificar la corrección total de la siguiente función:

function potencia(a: real; b: integer) dev p: real;

var x: real; y: integer;

begin

{ b ≥ 0 }

<x,y,p> := <a,b,1>;

while y > 0 do

begin

if impar(y) then z := z*x;

<x,y> := <x*x,y div 2>

end

end;

29. (*) Verificar la corrección total de la siguiente función:

function dividir(x,y: integer) dev r,q: integer;

var w: integer;

begin

{ x ≥ 0, y > 0 }

r := x; q := 0; w := y;

while w <=r do w := 2*w;

while w <> y do

begin

q := 2*q; w := w div 2;

if w <= r then

begin

r := r-w;

q := q+1

end

end;

30. (*) Verificar la corrección total de la siguiente función, averiguando qué es lo que hace:

function inc_ognita(n: integer) dev r: integer;

var

x,y : integer;

c1,c2 : boolean;

begin

{ n ≥ 0 }

<x,y,r,c1> := <n,1,0,true>;

while (x > 0) or c1 do

begin

c2 := impar(x);

if c1 <> c2 then r := r+y;

c1 := c1 and c2;

<x,y> := <x div 2,2*y>

end

31. (**) Demostrar la finitud de la siguiente función: (Nota: En la hoja de problemas la función aparece escrita de forma erronea. Esta es la función correcta).

function pedrisco(a: integer) dev n: integer;

var x : integer;

begin

{ a > 1 }

<n,x> := <0,a>;

while x > 1 do

begin

if impar(x) then x := 3*x+1 else x := x div 2;

n := n+1

end

end;

32. Verificar la corrección parcial de la siguiente función, cuyo objetivo es obtener el valor máximo de un array de enteros:

const N = ..;

function max(v: array[1..N] of integer) dev m: integer;

var i : integer;

begin

{ N > 1 }

m := v[1];

for i := 2 to N do

if v[i] > m then m := v[i];

{

α : 1 ≤ α ≤ N : m ≥ v_α }

end;

33. Verificar la corrección parcial de la siguiente función, cuyo objetivo es evaluar mediante el método de Horner el polinomio a_n·xⁿ + a_n-1·x^n-1 + ··· + a₁·x + a₀ para un determinado valor de x:

const N = ..;

function Horner(v: array[0..N] of real; x: real) dev r: real;

var i : integer;

begin

{ N ≥ 0 }

r := 0;

for i := N downto 0 do

r := v[i]+r*x;

{ r =

α : 0 ≤ α ≤ N : v_α·x^α }

end;

34. Verificar la corrección parcial del siguiente trozo de código que implementa una versión del algoritmo de ordenación por el método de la burbuja (se proporcionan candidatos a invariantes de los bucles):

const N = ..;

var

v : array[1..N] of integer;

i,j : integer;

...

for i := 1 to N-1 do

begin

for j := 1 to N-i do

begin

if v[j] > v[j+1] then <v[j],v[j+1]> := <v[j+1],v[j]>

{

α : 1 ≤ α < j : v_α ≤ v_j }

end

{

α : N-i+1 ≤ α ≤ N :

β : 1 ≤ β < α : v_β ≤ v_α }

end;

{

α : 1 ≤ α < N : v_α ≤ v_α+1 }

...

35. (*) Se desea crear una función cuyo objetivo sea realizar una búsqueda binaria de un valor, x, sobre el vector ordenado v para encontrar la primera posición del vector ocupada por un valor mayor que x.

Escribir la precondición y postcondición que deberían cumplirse. Escribir la cabecera y las cláusulas require y ensure de una función Eiffel que implementara esa función.
De acuerdo con la precondición y postcondición anteriores, desarrollar una batería de pruebas para esa función mediante el método de caja negra.
Verificar la corrección total de las siguientes implementaciones de esta función:

const N = ..;

function busq1(v: array[1..N] of real; x: real) dev p: integer;

var

izda,dcha,med: integer;

begin

{ N ≥ 0,

α : 1 ≤ α < N : v_α ≤ v_α+1 }

<izda,dcha> := <1,N>;

while izda <= dcha do

begin

med := (izda+dcha) div 2;

if v[med] < x then izda := med+1 else dcha := med-1;

end;

p := izda

end;

function busq2(v: array[1..N] of real; x: real) dev p: integer;

var

izda,dcha,med: integer;

begin

{ N ≥ 0,

α : 1 ≤ α < N : v_α ≤ v_α+1 }

<izda,dcha> := <1,N>;

while izda < dcha do

begin

med := (izda+dcha) div 2;

if v[med] < x then izda := med else dcha := med;

end;

p := dcha+1

end;