Búsqueda y Ordenación

1. Clasificar el siguiente vector:

   
   
   

    

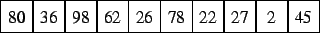
   1. Mediante el método de burbuja.
   2. Mediante el método de inserción.
   3. Mediante el método de selección.

   Para los tres casos mostrar las modificaciones que va sufriendo el vector según se va realizando la ordenación.

    

2. Escribir un algoritmo que lea diez nombres y los ponga en orden alfabético utilizando el método de selección.

    

3. Construir un algoritmo que permita la introducción de 10 números enteros en un vector y, a través de un menú, la selección de uno de los siguientes métodos de ordenación: selección, inserción o burbuja. Terminará con la presentación por pantalla del vector ordenado.

    

4. Desarrolle un procedimiento para ordenar una matriz de 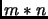considerando que el último elemento de cada fila y el primero de la siguiente son contiguos.

    

5. Ordenar de mayor a menor un vector de N elementos (N<=40), cada uno de los cuales es un registro con los campos día, mes y año de tipo entero.

   Utilice la función esMenor(fecha1,fecha2), que nos devuelva si una fecha es menor que la otra.

    

6. Dada la lista de fechas ordenada en orden decreciente del ejercicio anterior, diseñar dos procedimientos:

    

   1. Buscar, que nos informará sobre si una determinada fecha se encuentra o no en la lista:
      • si no está, indicará la posición donde correspondería insertarla.
      • si está, nos dirá la posición donde la hemos encontrado.
   2. Insertar, que nos permitirá insertar una fecha en una determinada posición.

    

7. Se dispone de una lista de números enteros clasificados en orden creciente. Se desea conocer si un número dado introducido desde el terminal se encuentra en la lista. En caso afirmativo, averiguar su posición y mostrarla por pantalla. En caso negativo se desea insertarlo en la posición adecuada y posteriormente mostrar la posición por pantalla.

    

8. Se desea comparar el funcionamiento de los diferentes métodos de búsqueda. Para ello se pretende buscar el número 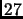en el siguiente vector:

   
   
   

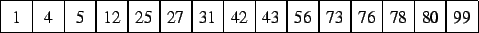
   Indique los pasos que seguirían los siguientes algoritmos:

    

   1. Búsqueda secuencial.
   2. Búsqueda binaria.

   Recursividad

    

9. Elaborar dos funciones en Pascal para calcular el factorial de un valor, una de ellas recursiva y la otra no.

    

10. Escribir una función recursiva Pascal para calcular el máximo común divisor de dos números enteros no nulos cualesquiera. Comparar el resultado con la solución no recursiva ya presentada en la asignatura.

     

11. El problema de las Torres de Hanoi consiste en lo siguiente: Hay tres postes; en uno se encuentra una torre con n discos, todos de diferentes tamaños, colocados del más grande en la base, hasta el más pequeño en la cima. Elaborar un programa que exhiba todos los pasos para mover la torre a otro poste, moviendo un solo disco cada vez, y sin colocar un disco más grande encima de otro menor.

     

12. (Examen curso 87/88). Escribir lo que devolvería la siguiente función recursiva con las llamadas concurso(0, 3), concurso(10, -7) y concurso(5, 5).

     

    function concurso(base, lim : integer) : integer;
    begin
       if base = lim
          then concurso := 1
       else if base > lim
             then concurso := 0
             else concurso := base + concurso(base+1, lim)
    end;
    

     

13. Se define la sucesión de Fibonacci de la siguiente forma : 0 1 1 2 3 5 8 13 21.... Escribir una función recursiva y otra no recursiva en Pascal para calcular el término n-ésimo de la sucesión de Fibonacci.

     

14. Elaborar una función que multiplique dos números naturales mayores que cero utilizando el siguiente método:

    
    

     

    
    
    

     

    
    

     

    
    
    

     

     

15. La función de Ackerman A se define para valores enteros no negativos m y n del siguiente modo:

    
    

     

    
    
    

     

    
    

     

    
    
    

     

    
    

     

    
    
    

     

    Definir una función recursiva en Pascal que implemente la función de Ackerman. Intentar encontrar una versión no recursiva.

     

16. Un laberinto se puede definir como un recinto rectangular formado por casillas cada una de las cuales puede estar libre o ocupada por un obstáculo. El perímetro del laberinto está formado por obstáculos excepto una o más salidas. Resolver el laberinto es encontrar un camino que lleve desde un punto inicial a una de las salidas, desplazándose siempre en sentido horizontal o vertical y exclusivamente por casillas libres. Elaborar un algoritmo capaz de resolver un laberinto.

     

17. El problema de las ocho reinas consiste en encontrar una disposición de ocho reinas en un tablero de ajedrez de tal manera que ninguna de ellas amenace a ninguna otra (en el juego del ajedrez una reina amenaza a cualquier pieza que le sea accesible mediante un desplazamiento horizontal, vertical o diagonal de cualquier número de casillas). Desarrollar un programa que nos muestre en pantalla la disposición de las reinas. Tras resolver el problema, intentar generalizarlo a los casos siguientes:

     

    • Colocar N reinas sobre un tablero de N filas y N columnas.
    • Encontrar no solo una solución, sino todas las soluciones posibles, mostrándolas sucesivamente en pantalla.
    • Elaborar un programa que nos diga el número de soluciones existentes para los tableros de dimensiones desde 1 x 1 hasta 11 x 11.

    Sugerencia: Como es evidente que debe haber una reina en cada fila, el problema de colocar N reinas en un tablero de N filas se puede definir de forma recursiva como el problema de colocar una reina en una determinada columna permitida de la primera fila y luego colocar N-1 reinas en el resto del tablero (N-1 filas). Por supuesto, las columnas permitidas en cada fila dependen de cómo estén colocadas las reinas de las filas anteriores.

     

18. (Examen curso 95/96) Se dispone de una matriz bidimensional de 100 x 100 elementos en la cual se almacena una imagen. Cada elemento de la matriz es un número entero que hace referencia a un determinado color en pantalla. Como parte de un de un programa de dibujo, se quiere desarrollar el siguiente procedimiento:

     

    procedure rellenar(var M: TMatriz; X, Y, NuevoColor: Integer)
    

    El cual debe realizar la tarea siguiente: Rellenar el área contigua a la posición de la matriz situada en la fila Y y la columna X con el valor dado por NuevoColor. Se define como área contigua a una casilla de la matriz todas aquellas casillas accesibles mediante movimientos verticales u horizontales (no en diagonal) y del mismo valor (color) que la casilla original.

    Ejemplo: rellenar(M,3,5,7) sobre la matriz de la izquierda produciría la matriz de la derecha

     

    1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 1 1 8 8 8 1 1 1 1 3 1 1 8 1 1 8 1 1 1 4 1 8 8 8 1 1 8 8 1 5 1 8 8 8 8 1 8 8 1 6 1 8 8 8 8 1 1 1 1 7 1 1 8 8 1 1 1 1 1 8 1 1 1 1 1 1 1 1 1

    1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 1 1 7 7 7 1 1 1 1 3 1 1 7 1 1 8 1 1 1 4 1 7 7 7 1 1 8 8 1 5 1 7 7 7 7 1 8 8 1 6 1 7 7 7 7 1 1 1 1 7 1 1 7 7 1 1 1 1 1 8 1 1 1 1 1 1 1 1 1

    Desarrollar un procedimiento en pascal que implemente esta operación.

Última modificación: martes, 07 de enero de 2003

Administrador: cesargf [at] infor.uva.es