Atención: Esta página está en construcción. A lo largo del curso iré incluyendo nuevas soluciones a los problemas y ampliando las existentes. Puede enviar dudas, sugerencias, solicitudes de resolución, etc., a la dirección cvaca@infor.uva.es.

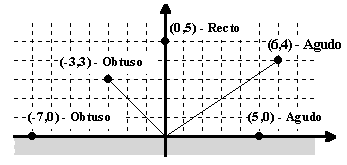
1. Se dispone de un módulo cuyo objetivo es clasificar como agudo, recto u obtuso el ángulo que forma una determinada linea con el eje horizontal. La linea se define como aquella que pasa por el origen de coordenadas y por un punto del semiplano superior. Las coordenadas de este punto son los valores que recibe el módulo como parámetro. Ejemplos:

Para que el módulo pueda calcular un valor correcto (agudo, recto, obtuso) las entradas deben cumplir los siguientes requisitos:

• El módulo debe recibir como entrada dos valores enteros, que representan las coordenadas horizontal y vertical, respectivamente, del punto anteriormente descrito.
• El punto pertenece al semiplano superior o al eje horizontal.
• El punto no es el origen de coordenadas (existirían infinitas lineas posibles).

Si no se cumplen los requisitos anteriores, el módulo devolverá el valor error. Elaborar una batería de pruebas por el método de caja negra para el módulo descrito.

Solución

2. Se dispone de un módulo, linea, cuyo objetivo es clasificar una linea según su inclinación como horizontal, vertical o inclinada. La linea se define como aquella que pasa por dos puntos dados, y cada punto se especifica mediante sus coordenadas horizontal y vertical. Ejemplos:

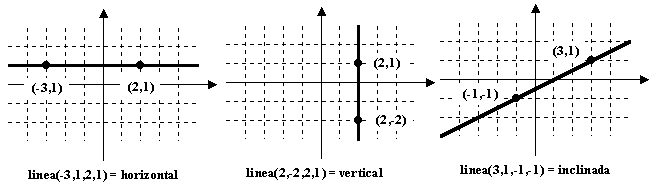
Para que el módulo pueda calcular un valor correcto (horizontal, vertical, inclinada) las entradas deben cumplir los siguientes requisitos:

• El módulo debe recibir como entrada cuatro valores enteros, que representan las coordenadas horizontal y vertical de los dos puntos que definen la linea (ver ejemplos).
• Los dos puntos no pueden ser iguales (la linea estaría indefinida).

Si no se cumplen los requisitos anteriores, el módulo devolverá el valor error. Elaborar una batería de pruebas por el método de caja negra para el módulo descrito.

3. Se dispone de un módulo, rectangulo, que recibe como entrada cuatro valores enteros, x₀, y₀, x₁ e y₁, que representan las coordenadas del vértice superior izquierda (x₀, y₀) y del vértice inferior derecho (x₁, y₁) que definen a un rectángulo, y que se encarga de detectar los casos especiales en que estas coordenadas corresponden a una linea horizontal (y₀ = y₁), linea vertical (x₀ = x₁), o a un punto (x₀ = x₁ e y₀ = y₁).

El módulo proporciona como salida un valor entero con el siguiente significado: 0 - punto, 1 - linea horizontal, 2 - linea vertical, 3 - rectángulo.

Obtener los casos de prueba resultantes de aplicar los métodos de caja negra y análisis de valores límite al módulo anterior. Como casos no válidos, además de los habituales, se encuentran aquellos en que las coordenadas de los vértices no corresponden a los puntos superior izquierda e inferior derecho (x₀ > x₁ o y₀ < y₁).

4. Disponemos de un módulo, busqueda, cuya función es buscar la aparición de un determinado valor entero dentro de un vector ordenado de enteros. En caso de encontrar el valor, el módulo devuelve la posición del vector donde se ha encontrado (se supone que al primer componente del vector le corresponde la posición 1, al segundo la posición 2, etc). En caso de no encontrarse dentro del vector, el módulo devuelve -1. Si existieran varias apariciones del valor buscado dentro del vector, el módulo devolverá la menor posición donde se encuentre.

Los parámetros del módulo son, en primer lugar el valor buscado, a continuación el vector y por último un valor entero que indica cual es el tamaño (número de componentes) del vector.

Ejemplo: busqueda(5, [1,3,3,5,5,5,9], 7) devolverá 4.

Se desconoce el lenguaje en que se ha implementado el módulo, y se consideran como casos no válidos (además de los habituales) aquellos en que el vector no se encuentre ordenado y cuando el tamaño del vector no corresponda realmente con el número de elementos que contiene.

Diseñar un conjunto de casos de prueba para el módulo anterior mediante pruebas de caja negra y análisis de valores límite.

Solución

5. Se desea probar un módulo que calcula el máximo común divisor de dos valores enteros mayores que cero que recibe como entrada. Se sabe que el módulo utiliza un algoritmo que requiere realizar comparaciones de igualdad, mayor y menor entre los parámetros.

Si el módulo recibe un número de parámetros distinto de dos, los tipos de los parámetros no son los adecuados o alguno de ellos es negativo o cero, el resultado devuelto por el módulo es el valor -1.

Crear la tabla de particiones de equivalencia y la batería de pruebas que se deriva de ella, añadiendo los casos de prueba adicionales obtenidos por el análisis de valores límite.

Solución

6. Diseñar un conjunto de casos de prueba para un módulo que recibe como entrada tres valores enteros que representan la longitud de los datos de un triángulo, y proporciona como salida la clasificación equilátero, isósceles, escaleno ó error. Este último valor corresponde a alguna de las situaciones siguientes:

• El número de parámetros es erroneo.
• El tipo de los parámetros es erroneo.
• Los valores no son positivos.
• Con los valores proporcionados no es posible construir un triángulo.

Solución

7. Elaborar una batería de pruebas para un módulo que recibe como entrada una cadena de caracteres y determina si puede ser una clave válida o no (por lo tanto devuelve un valor lógico, si o no). Una clave se considera válida si cumple los requisitos siguientes:

• Esta formada por más de 4 y menos de 8 carácteres.
• Los caracteres permitidos son las letras a..z, A..Z, los dígitos 0..9 y el carácter %.
• Contiene al menos dos letras.
• Contiene al menos un carácter que no es letra.
• El primer y último carácter son letras.
• No aparece en un diccionario de palabras prohibidas (user%10a, user%aa, ..).

Solución

8. Se dispone de un módulo que recibe como entrada dos parámetros enteros, a y b. El objetivo del módulo es determinar si b divide exactamente a a. Las salidas posibles del módulo son:

• IGUALES: Si ambos valores son iguales.
• CONGRUENTE: Si b divide exactamente a a y ambos valores no son iguales.
• INCONGRUENTE: Si b no divide exactamente a a.
• ERROR: Si las entradas del módulo son erróneas.

Además de los casos habituales, se considera como errónea una entrada en la que b sea nulo.

Diseñar un conjunto de casos de prueba para el módulo anterior mediante pruebas de caja negra y análisis de valores límite.