Problema 1

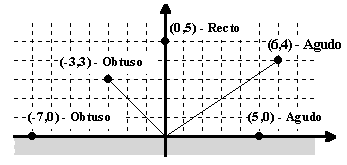
1. Se dispone de un módulo cuyo objetivo es clasificar como agudo, recto u obtuso el ángulo que forma una determinada linea con el eje horizontal. La linea se define como aquella que pasa por el origen de coordenadas y por un punto del semiplano superior. Las coordenadas de este punto son los valores que recibe el módulo como parámetro. Ejemplos:

Para que el módulo pueda calcular un valor correcto (agudo, recto, obtuso) las entradas deben cumplir los siguientes requisitos:

• El módulo debe recibir como entrada dos valores enteros, que representan las coordenadas horizontal y vertical, respectivamente, del punto anteriormente descrito.
• El punto pertenece al semiplano superior o al eje horizontal.
• El punto no es el origen de coordenadas (existirían infinitas lineas posibles).

Si no se cumplen los requisitos anteriores, el módulo devolverá el valor error. Elaborar una batería de pruebas por el método de caja negra para el módulo descrito.

Las condiciones que separan entradas correctas de entradas erroneas son el número de parámetros, el tipo de los parámetros, que el punto pertenezca al semiplano superior y que no sea el origen. Parece lógico que se compruebe que no sea el origen antes de comprobar que pertenezca al semiplano superior, ya que la primera condición es más general que la segunda.

Ya que el módulo clasifica un ángulo, se supondrá que entradas que dan lugar a resultados distintos se tratan de forma diferenciada en el módulo, lo que da lugar a tres condiciones según la entrada pertenezca al semiplano derecho (ángulo agudo), a la ordenada vertical (ángulo recto) o al semiplano izquierdo (ángulo obtuso). Para estas condiciones, lo mínimo que se puede asumir es que el número y tipo de los parámetros es el adecuado.

La tabla de particiones de equivalencia resultante sería la siguiente:

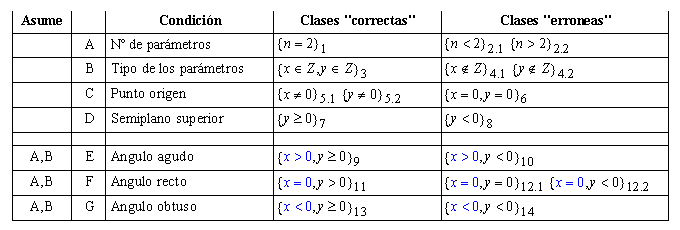
En principio, ya que las clases 5.1 y 5.2 expresan desigualdad respecto a un valor constante, se deberían subdividir en comparaciones de mayor y menor, al igual que se ha hecho con las clases 2.1 y 2.2. En ese caso obtendríamos lo siguiente:

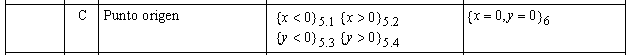
El objetivo de esa división es obtener casos de prueba separados para entradas con un valor mayor y menor que esa constante. Sin embargo, en este problema podemos ver que esa separación ya se da, para 5.1 y 5.2 en las clases 9 y 13, y para 5.3 y 5.4 en las clases 7 y 8, por lo que en este caso no es necesario realizar la subdivisión.

Por otro lado, la condición de la clase 9 estaría compuesta por la condición de ángulo agudo (x < 0) junto con las condiciones de las clases 5.1-5.2 y 7 (no asumidas), lo que daría lugar a 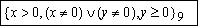. Simplificando esa expresión (que x sea mayor que cero garantiza que no es el origen) es como se obtiene la condición que aparece en la tabla. El mismo razonamiento se aplica a la clase 13.

Igualmente, la condición original de la clase 11 sería 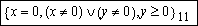, que se simplifica 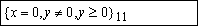a . En la tabla se escribe de manera más compacta, pero esta es la expresión que sirve de base para obtener las clases "erroneas" que aparecen en la tabla, 12.1 y 12.2 (por eso se obtienen dos clases en lugar de una).

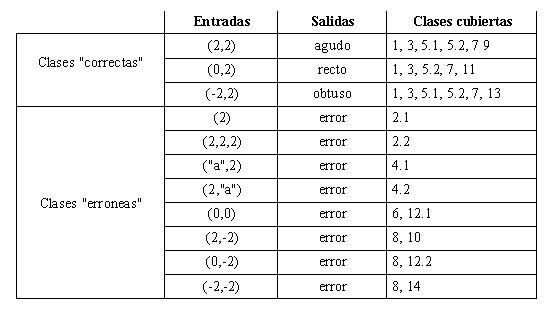
De la tabla de particiones se obtiene la siguiente batería de pruebas:

Regresar a la página de enunciados.