Problema 11
11. Resolver el problema de las torres de Hanoi con cuatro postes. Evaluar el orden del algoritmo y comprobar si supone una mejora respecto al problema con tres postes. Verificar si es posible aplicar una estrategia divide y vencerás al problema.
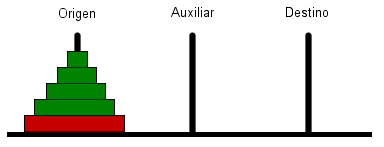
Observando el esquema de resolución de las torres de Hanoi con tres postes, es relativamente sencillo generalizarlo al problema de cuatro (o más) postes. El algoritmo para resolver el problema con tres postes se muestra en la siguiente animación:

El algoritmo resuelve el problema de mover n discos poniendoló en función de la resolución del problema (más sencillo) de mover n-1 discos. El siguiente procedimiento muestra la solución imprimiendo una serie de lineas que indican el disco que hay que mover en cada momento (se supone que los postes se identifican por un carácter):
procedure Hanoi3(N: integer; Orig,Dest,Aux: char);
begin
if N = 1 then
writeln(output,Orig,' -> ',Dest)
else
begin
Hanoi3(N-1,Orig,Aux,Dest);
writeln(output,Orig,' -> ',Dest);
Hanoi3(N-1,Aux,Dest,Orig)
end
end;
Si estamos interesados en medir el algoritmo en función del número de movimientos (sentencias writeln) necesarios para resolver el problema, obtenemos la siguiente relación de recurrencia:
| T(1) = 1 | Þ | T(n) Î Q(2n) |
| T(n) = 2·T(n-1) + 2 |
Si disponemos de 4 postes, se pueden desplazar (recursivamente) n-2 discos a un poste auxiliar, y ahora somos capaces (debido al poste adicional) de mover los dos discos restantes al poste destino. Lo que se gana respecto al problema anterior es que el subproblema es de menor tamaño, mover n-2 discos en lugar de n-1. La siguiente animación muestra como se comportaría el algoritmo:
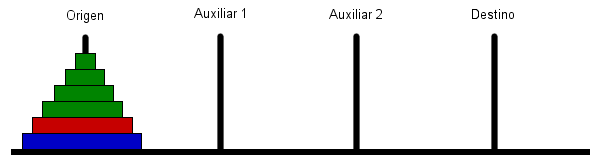
Este algoritmo se podría implementar de la siguiente forma:
procedure Hanoi4(N: integer; Orig,Dest,Aux1,Aux2: char);
begin
if N = 0 then
{ En este caso base no se hace nada }
else if N = 1 then
writeln(output,Orig,' -> ',Dest)
else
begin
Hanoi4(N-2,Orig,Aux1,Dest,Aux2);
writeln(output,Orig,' -> ',Aux2);
writeln(output,Orig,' -> ',Dest);
writeln(output,Aux2,' -> ',Dest);
Hanoi4(N-2,Aux1,Dest,Orig,Aux2)
end
end;
Ahora tenemos dos casos base, cuando n = 0 (en cuyo caso no hay que hacer nada) y cuando n = 1 (mover un único disco). Aunque el código podría haberse escrito de manera más compacta (y sería más eficiente si en lugar de considerar como caso base n = 0 hubieramos elegido n = 2), he elegido dejarlo así para mostrar claramente la idea del algoritmo.
Las relaciones de recurrencia que se obtienen son:
| T(0) = 0 | Þ | T(n) Î Q(2n/2) |
| T(1) = 1 | ||
| T(n) = 2·T(n-2) + 3 |
Vemos que el orden mejora (aunque sigue siendo no polinómico), ya que es menor un orden Q(2n/2) que un orden Q(2n).
Para aplicar una estrategia divide y vencerás al problema sería necesario que los subproblemas tuvieran un tamaño aproximadamente mitad, es decir, debemos espresar la solución en función de mover n/2 discos.
El mover los n/2 discos superiores no plantea dificultades, ya que se dispone de cuatro postes accesibles. Sin embargo, al mover los n/2 discos inferiores sólo disponemos de tres postes, ya que uno no es accesible al contener la subtorre con los n/2 discos superiores.
Una forma de afrontar el problema es mover los n/2 discos inferiores utilizando el algoritmo de las torres de Hanoi con tres postes. De esa forma, el algoritmo utilizado sería el que se muestra en la animación:
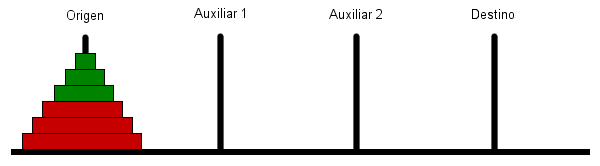
Este algoritmo se podría implementar de la siguiente forma:
procedure Hanoi4(N: integer; Orig,Dest,Aux1,Aux2: char);
var M : integer;
begin
if N = 0 then
{ En este caso base no se hace nada }
else if N = 1 then
writeln(output,Orig,' -> ',Dest)
else
begin
M := N div 2;
Hanoi4(N-M,Orig,Aux1,Dest,Aux2);
Hanoi3(M,Orig,Dest,Aux2);
Hanoi4(N-M,Aux1,Dest,Orig,Aux2)
end
end;
La relación de recurrencia que se obtiene ahora es:
| T(0) = 0 |
| T(1) = 1 |
| T(n) = 2·T(n/2) + Q(2n) |
Esta relación no se puede ajustar a los esquemas disponibles, por lo que no se puede calcular el orden del algoritmo.
Regresar a la página de enunciados.