I.T.I. Sistemas - Programación II - Curso 00/01
Problemas de análisis y diseño de algoritmos.
Atención: Esta página está en construcción. A lo largo del curso iré incluyendo nuevas soluciones a los problemas y ampliando las existentes. Puede enviar dudas, sugerencias, solicitudes de resolución, etc., a la dirección cvaca@infor.uva.es.
1. Un programador ha implementado un algoritmo que tarda, en su antiguo ordenador de 100 Mhz, una milésima de segundo en resolver un problema de tamaño n = 20. ¿Cuanto tardaría en resolver un problema de tamaño n = 30 en los siguientes casos?
¿Por que factor debería multiplicar la velocidad de su ordenador para que volviera a tardar una milésima de segundo? Nota: 1 año = 31.557.600 segundos.
2. ¿Es posible que un algoritmo de orden O(n2) se ejecute más rapidamente que un algoritmo de orden O(n) en los siguientes casos?
3. Para el problema P se sabe que su complejidad en el peor caso es O(n2) y W(n lg n). Si A es un algoritmo que resuelve el problema P, ¿Cuáles de las siguientes opciones son consistentes con la información anterior?
4. Analizar cual sería el orden de complejidad del algoritmo que usamos habitualmente para multiplicar dos números enteros. Se supondrá que los dos números tienen el mismo número de dígitos, n, y que este valor define el tamaño de la entrada. Contar únicamente las operaciones de producto y suma de dígitos individuales.
5. Analizar el número de operaciones en las que interviene un elemento del vector en el siguiente algoritmo (ordenación por selección):
type TVector = array[1..N] of real;
procedure ordenar(var V: TVector);
var
I,J,Min : integer;
Temp : real;
begin
for I := 1 to N-1 do
begin
Min := I;
for J := I+1 to N do
if V[J] < V[Min] then Min := J;
Temp := V[I];
V[I] := V[Min];
V[Min] := Temp
end
end
Encontrar las fórmulas exactas para el peor y el mejor caso, identificar cuales son los tipos de entradas que producen esos casos y repetir el análisis utilizando notación asintótica.
6. Calcular, usando notación asintótica, el número de operaciones de incremento de x que realizan los siguientes fragmentos de programas:
for i := 1 to n do
for j := 1 to n do
if j = i then
x := x+1
for i := 1 to n do
for j := n downto i do
for k := i to j do
x := x+1
for i := 1 to n do
for j := 1 to i*i do
for k := 1 to j*j do
x := x+1
7. Calcular el orden de complejidad de las siguientes funciones recursivas (contar sólo las operaciones producto):
function f1(n: integer) : integer;
begin
if n < 1 then f1 := 1 else f1 := f1(n-3)*f1(n-3)
end;
function f2(n: integer) : integer;
begin
if n < 1 then f2 := 1 else
f2 := f2(n div 2)*f2(n div 2)*f2(n div 2)
end;
function f3(n: integer) : integer;
var i,x : integer;
begin
if n < 1 then f3 := 1 else
begin
x := 1;
for i := 1 to n do x := x*n;
f3 := x*f3(n-1)
end
end
function f4(n: integer) : integer;
var i,x : integer;
begin
if n < 1 then f4 := 1 else
begin
x := 1;
for i := 1 to n*n do x := x*2;
f4 := x*f4(n div 2)
end
end
8. Demostrar si los siguientes enunciados son ciertos o falsos:
Nota: Para el último caso puede ser conveniente utilizar el método de inducción: Suponer que es cierto para un determinado valor de n y demostrar que eso implica necesariamente que la expresión es cierta para n+1.
9. El algoritmo de búsqueda ternaria es similar a la búsqueda binaria pero se diferencia en que en cada etapa el subvector se divide en tres partes iguales (en lugar de dos) y se examinan los dos elementos que separan estas tres partes para decidir si se ha encontrado el valor o, en caso contrario, elegir una de estas tres partes para continuar la búsqueda en ella.
Analizar cuál sería la complejidad de este algoritmo para las operaciones en que interviene un elemento del vector (se puede suponer que el tamaño del vector es una potencia de tres) y comprobar si mejora o no el orden de la búsqueda binaria.
10. El problema de evaluar la expresión ab donde a es un valor real y b un entero positivo se puede resolver mediante un bucle donde se evalue b veces el producto de a, o bien es posible aplicar la siguiente fórmula en un esquema divide y vencerás:
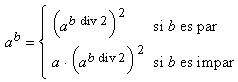
Desarrollar algoritmos para ambas soluciones y evaluar el orden de complejidad de cada uno tomando como tamaño de la entrada el número de bits del exponente, b.
11. Resolver el problema de las torres de Hanoi con cuatro postes. Evaluar el orden del algoritmo y comprobar si supone una mejora respecto al problema con tres postes. Verificar si es posible aplicar una estrategia divide y vencerás al problema.
12. Resolver el problema de las torres de Hanoi con tres postes cuando se parte de cualquier posición válida. Sugerencia: Encontrar primero un esbozo de solución y diseñar despues el tipo de datos que represente la posición de los discos que sea más adecuado para esa forma de resolver el problema. Evaluar el orden del algoritmo obtenido.
13. Se dispone de una matriz de tipo TLaberinto:
type
TCasilla = (pared,libre,marca);
TLaberinto = array[1..N,1..N] of TCasilla;
La cual representa un laberinto donde desde una casilla es posible acceder a cualquier casilla adyacente (superior, inferior, izquierda y derecha) que tenga el valor libre o marca. Inicialmente se proporciona la matriz que define el laberinto donde las casillas tienen los valores libre o pared, y la fila y columna de partida.
Desarrollar un algoritmo que indique si existe o no un camino para salir del laberinto partiendo de la posición inicial y pasando únicamente por casillas marcadas inicialmente como libres. Salir del laberinto significa alcanzar un casilla libre en los límites de la matriz. Si la posición inicial está fuera del laberinto o corresponde a una casilla con valor pared, la respuesta sera falso.
Nota: Se permite modificar el contenido de la matriz haciendo uso del valor marca con el propósito de no volver a pasar por una casilla ya recorrida.
Modificar el algoritmo obtenido para que, en el caso de que exista una solución, imprima las filas y columnas de las casillas que se deben recorrer para salir del laberinto.
14. Dado un número entero n se desea obtener todas las posibles formas de expresarlo como sumas de los enteros 1 .. n, permitiendo que el mismo sumando aparezca varias veces. Se considerarán iguales (y por lo tanto sólo se debe escribir una de ellas) aquellas soluciones que contengan los mismos sumandos pero ordenados de otra manera. Por ejemplo, si n = 4, se deberían escribir las soluciones 4=1+1+1+1, 4=2+1+2, 4=2+2, 4=3+1, 4=4.
Crear un algoritmo que resuelva el problema. No importa el orden en que aparecen las soluciones ni el orden de los sumandos dentro de cada solución.
15. Crear un programa que lea una cadena de caracteres, compruebe no existe en ella ningún carácter repetido, y en ese caso escriba todas las cadenas que se pueden formar por permutaciones de los caracteres de la cadena original. Por ejemplo, si la cadena leida fuera "DATO", el programa escribiría:
| DATO | DAOT | DTAO | DTOA | DOAT | DOTA |
| ADTO | ADOT | ATDO | ATOD | AODT | AOTD |
| TDAO | TDOA | TADO | TAOD | TODA | TOAD |
| ODAT | ODTA | OADT | OATD | OTDA | OTAD |
16. El problema las n reinas consiste en colocar n reinas sobre un tablero de ajedrez de n x n casillas de tal forma que ninguna reina pueda amenazar a otra. Aplicando la tecnica de backtracking crear un algoritmo que, dado un valor de n entre 1 y 12:
Diseñar los tipos de datos más adecuados para facilitar la operación de comprobar si una casilla es accesible a alguna de las reinas dispuestas en el tablero.
17. Se dispone de un tablero de ajedrez de n x n casillas. El problema del recorrido del caballo consiste en encontrar una forma de recorrer, comenzando en la casilla (1,1), todas las casillas del tablero pasando de una a otra mediante saltos de caballo y sin pasar más de una vez por cada casilla. Crear un algoritmo que resuelva el problema.
18. Analizar cómo se podría aplicar la estrategia divide y vencerás al problema de multiplicar dos números positivos de n bytes de longitud. Se puede suponer que los números están almacenados en vectores cuyos elementos son de tipo byte y que n (el tamaño de los vectores) es potencia de dos.
Analizar el orden asintótico del algoritmo anterior y compararlo con el algoritmo clásico de multiplicación. Sólo es necesario contar las operaciones de suma, resta y producto entre valores de tipo byte, y todas ellas miden lo mismo.
19. Crear un algoritmo recursivo que escriba por pantalla un valor n en base b (2 £ b £ 10). Estimar el orden de complejidad del algoritmo en función del número de dígitos de n, contando las operaciones de resta y división. Aplicar la estrategia divide y vencerás al algoritmo anterior y comprobar si mejora el orden asintótico obtenido.
20. El problema de la mochila 0/1. En este problema disponemos de dos vectores, v1, v2, .., vn y p1, p2, ..., pn, que indican, respectivamente, el valor y el peso de cada uno de n objetos. El objetivo es decidir, para cada objeto, si lo incluimos o no en una mochila cuya capacidad máxima es M kilos. De entre todas las maneras distintas de llenar la mochila sin superar ese límite, debemos escojer aquella que proporcione la mochila más valiosa.
Es decir, si expresamos la solución como el vector x1, x2, ..., xn donde xi = 1 indica que el objeto i se incluye en la mochila y xi = 0 indica que el objeto i no se incluye, se debe cumplir que:
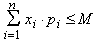(restricción), y que 
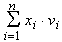(valor de la mochila) es máximo.
Resolver este problema utilizando backtracking y estimar el orden de complejidad en el peor caso, contando las operaciones en que se acceda a vectores.
21. Se dispone de una secuencia de n enteros, v1,v2,...,vn, y se desea hallar la subsecuencia cuya suma sea máxima. Por ejemplo, dada la secuencia -2, 10, 5, -3, 4, -6, -2, 7 la subsecuencia de suma máxima es la comprendida entre los índices 2 y 5 (10, 5, -3, 4).