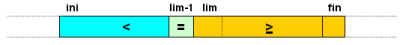Preguntas más frecuentes sobre la práctica
|
En ésta página ire respondiendo a las preguntas cuya respuesta
sea de interés general para aquellos que trabajen en la práctica.
Podeís hacerme preguntas (además de personalmente) utilizando el
correo electrónico (cvaca@infor.uva.es)
o bien mediante el Foro de la asignatura.
Contenido: (actualizado el 3 de mayo de 2004)
¿Donde se puede obtener información adiccional sobre Eiffel?
En la siguiente dirección
archive.eiffel.com/doc/online/eiffel50/intro se puede acceder a tutoriales para
aprender a programar en Eiffel.
La documentación incluida en GNU Eiffel la podeis descargar directamente
pulsando aquí.
¿Donde puedo obtener un compilador de Eiffel?
Existen varias versiones de Eiffel, tanto para Linux como Windows. En la página
principal de Eiffel (smarteiffel.loria.fr)
podeis encontrar las últimas versiones de libre distribución.
El compilador GNU Eiffel (SmallEiffel versión -0.72) para Windows lo podeis
descargar directamente desde ésta página
pulsando aquí (Tamaño: 10 megas).
¿Que clases de la librería estandar puedo utilizar?
Las clases descritas en las guias de Eiffel (tipos simples y STRING, ARRAY,
TEXT_FILE_READ y TEXT_FILE_WRITE) son suficientes para poder realizar la práctica.
Se puede usar cualquier método de esas clases, no sólo los mencionados
en las guias. Si alguien desea utilizar otras clases debe comunicarmelo previamente.
Para saber cuales son los métodos de una clase, se escribe en una
consola el comando:
short clase | more
Donde clase es el nombre de la clase por la que se pregunta
(por ejemplo ARRAY).
Problemas al leer caracteres por teclado
Se aconseja que la lectura de caracteres se realice usando el método
read_line en lugar de read_character, ya
que realmente lo que se desea es leer una linea y obtener su primer carácter.
De esa forma se evitan problemas derivados del hecho de que el retorno de linea
consiste en uno o varios caracteres y además se puede detectar si el usuario
ha dejado la linea en blanco.
Por ejemplo, para obtener el carácter en la variable ch de
tipo CHARACTER escribiríamos el siguiente código:
io.read_line
if io.last_string.count = 0 then ch := '%U' else ch := io.last_string.item(1) end
No se puede concatenar una cadena con un carácter
No. A diferencia de Pascal, Eiffel no convierte automaticamente un valor de tipos
CHARACTER en STRING y el operador concatenar sólo admite
parámetros de tipo STRING. Si lo que se desea es añadir un
carácter al final de una cadena se puede hacer mediante el método
add_last(c: CHARACTER) de la clase STRING.
Sin embargo, si quiere hacer algo parecido a esto (ch es una variable de tipo CHARACTER):
io.put_string("El caracter seleccionado es ["+ch+"]%N");
debe expresarlo de la siguiente manera:
io.put_string("El caracter seleccionado es [");
io.put_character(ch);
io.put_string("]%N");
Error en inspect si la expresión no pertenece a ningún rango
Efectivamente, la estructura de control inspect de Eiffel produce un error de ejecución si
el valor de la expresión no pertenece a ninguno de los rangos y no existe parte else. Si lo que
se desea es no hacer nada en esa situación se debe incluir una parte else vacía (sin
sentencias):
inspect ch
when '0' then ...
when '1' then ...
...
else -- no se escribe ninguna sentencia aqui
end -- inspect
¿Como se puede "vaciar" un array o cadena de caracteres?
Una posibilidad puede ser asignar un array o cadena vacíos:
vec := <<>>;
cad := "";
Sin embargo, las sentencias anteriores lo que hacen es crear nuevos objetos de tipos ARRAY
y STRING de longitud cero y asignar sus referencias a las variables. Los objetos
anteriores se pierden (y serán borrados por el recolector de basura).
Es mejor reutilizar los objetos existentes, y para ello existe el método
clear de la clase ARRAY y STRING cuyo objetivo es
cambiar la longitud del array o cadena de caracteres a cero, y por lo tanto pasan a estar
vacíos:
vec.clear;
cad.clear;
Problemas al copiar el fichero en un vector de cadenas
Hay que tener en cuenta los puntos siguientes:
- Un array de strings es en realidad un array que almacena referencias a
objetos cuya clase es
STRING. Si un array debe almacenar 1000 strings,
en algun punto se deben crear esos 1000 objetos, el mero hecho de crear un array
de tamaño 1000 sólo significa que hay espacio para almacenar 1000 referencias
a objetos, no que se hayan creado 1000 objetos.
- Una excepción a lo anterior es cuando utilizamos clases expandidas,
como
INTEGER, DOUBLE, BOOLEAN, CHARACTER, etc. Si creamos un array
de enteros de tamaño 1000 entonces si que se han creado 1000 objetos de
clase INTEGER.
- Las clases
TEXT_FILE_READ y STD_INPUT_OUPUT (que es la clase a
la que pertenece la variable io que usamos para leer de teclado y
escribir en pantalla) heredan de la clase INPUT_STREAM, donde están
definidos los métodos de lectura de datos, entre ellos read_line y
last_string.
- Cuando se llama a
read_line se lee una linea de texto y su contenido se
almacena en el atributo last_string, pero no se crea un nuevo
objeto STRING sino que se cambia el contenido del objeto STRING
al que apunta last_string. Es decir, que cuando se crea un objeto INPUT_STREAM
(por ejemplo un fichero) se crea un objeto STRING cuya referencia almacena
el atributo last_string y a partir de entonces la referencia que almacena
last_string ya no cambia. Cuando se llama a read_line simplemente
se cambia el contenido del objeto referenciado por last_string.
Por eso un código como el que se muestra a continuación es erroneo:
fichero_a_vector(nom_fich: STRING) : ARRAY[STRING] is
-- Devuelve un vector que contiene las lineas de un fichero de texto
-- (una linea en cada posición)
local
fich : TEXT_FILE_READ;
do
-- Se crea el vector
create Result.with_capacity(100,1);
-- Se crea el fichero
create fich.make;
fich.connect_to(nom_fich);
if fich.is_connected then
from until fich.end_of_input loop
-- Se lee una linea del fichero
fich.read_line;
-- Se añade al vector resultado
Result.add_last(fich.last_string);
end
fich.disconnect;
else
io.put_string("No se ha podido abrir el fichero!%N")
end
end -- fichero_a_vector
Lo que hace el código anterior es añadir la misma referencia (la del objeto
STRING referenciado por fich.last_string) en todas las posiciones
del vector. Por lo tanto todas las posiciones del vector almacenarán lo mismo, la referencia
a una cadena de texto cuyo contenido es la última linea leida del fichero.
Lo que hay que hacer es crear un nuevo objeto STRING por cada linea leida
del fichero, y hacer que su contenido sea igual al del objeto fich.last_string.
La referencia a ese nuevo objeto es lo que se debe almacenar en el vector:
fichero_a_vector(nom_fich: STRING) : ARRAY[STRING] is
-- Devuelve un vector que contiene las lineas de un fichero de texto
-- (una linea en cada posición)
local
fich : TEXT_FILE_READ;
linea : STRING;
do
-- Se crea el vector
create Result.with_capacity(100,1);
-- Se crea el fichero
create fich.make;
fich.connect_to(nom_fich);
if fich.is_connected then
from until fich.end_of_input loop
-- Se lee una linea del fichero
fich.read_line;
-- Se crea el objeto cadena que almacenará la linea
create linea.make_empty;
-- Se copia el contenido de la linea leída en la cadena
linea.copy(fich.last_string);
-- Se añade al vector resultado
Result.add_last(linea);
end
fich.disconnect;
else
io.put_string("No se ha podido abrir el fichero!%N")
end
end -- fichero_a_vector
Si el vector no está ordenado, es inevitable tener que hacer una búsqueda
secuencial (recorrer el vector hasta encontrar un elemento igual). La clase ARRAY
tiene metodos para hacer este tipo de búsqueda: index_of(elemento: like item): INTEGER
devuelve la posición del primer elemento del vector igual en contenido al que
se proporciona como parámetro, o bien un valor fuera del rango del vector si no hay ninguno
igual. Para la comparación de igualdad se utiliza el método is_equal
del elemento. El método fast_index_of(elemento: like item): INTEGER
funciona de la misma manero excepto que las comparaciones se hacen por referencia (usando
el operador =), no por contenido, por lo que devuelve la primera posición del vector que
apunta al mismo objeto apuntado por el parámetro.
El tiempo promedio de una búsqueda secuencial es proporcional al número de
elementos del vector. Si el vector está ordenado se puede usar una estrategia
mucho más eficiente, el algoritmo de búsqueda binaria o dicotómica,
que seguramente ya conoceis. Además, si lo que queremos es encontrar todos los
elementos del vector iguales a uno dado, al estar el vector ordenado lo único que debemos
hacer es encontrar la posición del primer elemento igual y los demás elementos
iguales estarán justo despues de él.
El algoritmo que deseamos debe proporcionarnos el índice del primer elemento que
sea mayor o igual que el buscado. Para ello usaremos dos variables, izda y
dcha, para señalar la zona del vector donde se realiza la búsqueda
de esa posición. En todo momento los elementos anteriores a izda serán
menores que el valor buscado y los elementos posteriores a dcha serán
mayores o iguales al valor buscado, tal como se muestra en la imagen:

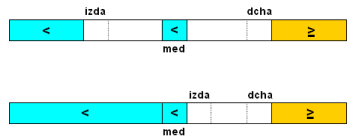
Para restringir la zona del vector donde se busca, comparamos el elemento medio de
la zona delimitada por izda y dcha. Si ese elemento es menor, entonces
todos los anteriores también lo serán (por ser un vector ordenado), y adaptamos
el valor de izda de la siguiente forma:
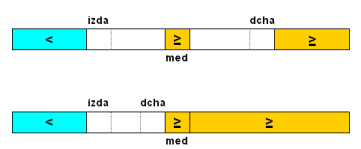
En caso contrario (el elemento medio es mayor o igual) adaptamos el valor de dcha:
Al final la zona a buscar será vacía (izda pasa a ser una unidad
mayor que dcha), y el vector pasa a estar clasificado de la siguiente forma:

El indice del primer elemento mayor o igual será entonces el valor de izda.
El código para implementar el algoritmo anterior sería el siguiente:
busqueda(vec: ARRAY[COMPARABLE]; val: COMPARABLE): INTEGER is
-- Devuelve la menor posición del vector que contiene un valor igual o mayor que val.
-- Si todos los elementos son menores que val o el vector está vacío
-- devuelve la posición siguiente a la última del vector.
local
izda,dcha,med : INTEGER;
do
from
izda := vec.lower;
dcha := vec.upper;
until izda > dcha loop
med := (izda+dcha)//2;
if vec.item(med) < val then
izda := med+1
else
dcha := med-1
end
end
Result := izda
end -- busqueda
Existen varios algoritmos para ordenar un vector, posiblemente conozcais el
algoritmo de ordenación por inserción o alguna de sus variantes. El
problema es que el tiempo que tarda ese algoritmo es proporcional al cuadrado del
tamaño (número de elementos) del vector, y por lo tanto es muy lento
para vectores con muchos elementos.
Voy a explicar otro algoritmo, la ordenación rápida (Quicksort)
que tiene un comportamiento mucho mejor (a efectos prácticos el tiempo
varía como el tamaño del vector multiplicado por su logaritmo). Para
un vector de 30000 elementos éste algoritmo es unas 700 veces más
rápido que la ordenación por inserción.
El algoritmo esta basado en realizar particiones del vector de
manera recursiva. Una partición consiste en elegir un
elemento del (sub)vector, que llamaremos el elemento pivote (en
principio vale cualquiera, nosotros escogeremos el que se encuentra en medio)
y reorganizar el vector, intercambiando elementos entre sí, de manera
que a la izquierda del vector queden los elementos menores (o iguales) que
el pivote, a la derecha los elementos mayores (o iguales) que el pivote y el
elemento pivote entre esas dos zonas. Ejemplo:
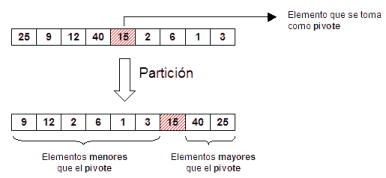
- La partición divide el vector en tres zonas: La de elementos
menores que el pivote, el propio pivote, y la de elementos mayores que el
pivote.
- Las zonas de menores o mayores no tienen porque estar ordenadas ni
tampoco es necesario que se mantenga el orden original.
- Es perfectamente posible que alguna zona quede vacía si da
la casualidad de que el pivote es el elemento máximo o mínimo.
La idea clave de la ordenación rápida consiste en aplicar la tecnica
divide y vencerás: Dividir el problema en partes y resolverlas por separado.
En este caso consistiría en ordenar el vector mediante la ordenación de
partes más pequeñas del vector. Si directamente dividimos el vector en
dos mitades y las ordenamos por separado, con ello no conseguimos obtener el vector
ordenado, tal como se muestra en el ejemplo:
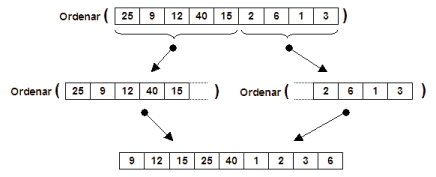
Sin embargo, si primero hacemos una partición en el vector y despues ordenamos
por separado la zona de menores y la zona de mayores, entonces si conseguimos obtener
un vector ordenado:
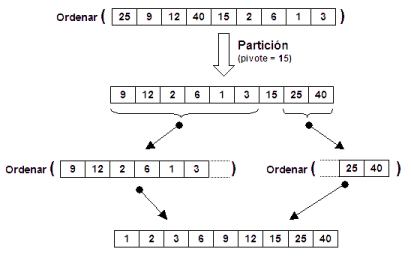
Para que éste método proporcione una ventaja en cuanto a eficiencia
es necesario que las ordenaciones sobre partes del vector sean recursivas, es
decir que a su vez realicen una partición y ordenen las partes que se obtengan.
El caso base de la recursividad se dará cuando obtengamos partes con uno o
ningún elemento en ellas: En esos casos no hay que hacer nada pues ya están
ordenadas.
El código para realizar la ordenación sería:
ordenar(vec: ARRAY[COMPARABLE]) is
-- Ordena el vector vec de menor a mayor por el algoritmo quicksort
do
if vec.count > 1 then
quicksort(vec,vec.lower,vec.upper)
end
end -- ordenar
quicksort(vec: ARRAY[COMPARABLE]; ini,fin: INTEGER) is
-- Ordena el subvector vec[ini..fin] de menor a mayor.
local
pos_piv : INTEGER;
do
pos_piv := particion(vec,ini,fin,(ini+fin) // 2);
if pos_piv > ini then quicksort(vec,ini,pos_piv-1) end
if pos_piv < fin then quicksort(vec,pos_piv+1,fin) end
end -- quicksort
Aplicado al ejemplo anterior, el proceso de ordenación sería el siguiente:
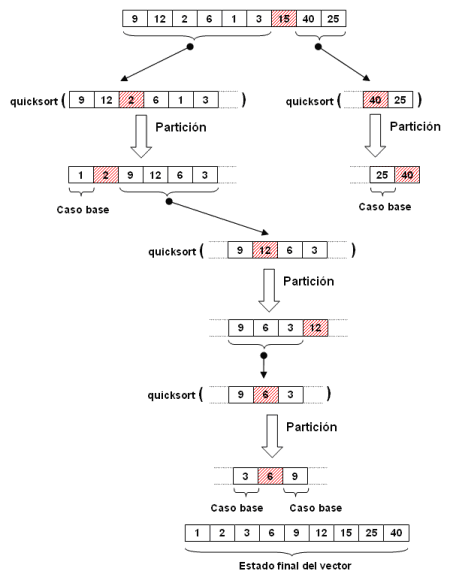
El método que realiza la partición recibe como parámetros el (sub)vector y la
posición del elemento que se utiliza como pivote, reorganiza los elementos y devuelve la nueva
posición del pivote. Los elementos anteriores a esa nueva posición serán menores
o iguales y los posteriores mayores o iguales.
Existen varios algoritmos para realizar la partición. Uno de los más sencillos
consiste en recorrer el subvector de manera que la zona por la que ya se ha pasado esté
organizada con los menores a la izquierda y los mayores o iguales a la derecha. Para ello primero
movemos el pivote a la primera posición (para que no moleste) mediante un intercambio:

Recorremos mediante un bucle, usando la variable i las posiciones desde
ini+1 hasta fin. En cada iteración se debe cumplir que en
la zona recorrida del vector (ini+1..i-1) los menores estén a la izquierda
y los mayores o iguales a la derecha. Usamos una variable, lim, para saber cual
es el primer elemento de la zona de mayores o iguales:

Comprobamos el elemento apuntado por i. Si es mayor o igual que el pivote
no hacemos nada (esta en la zona adecuada):

Si es menor que el pivote, entonces lo intercambiamos con el primero de la zona de
mayores o iguales (cuya posición almacena lim) e incrementamos el
valor de lim:
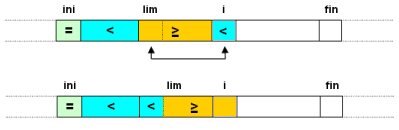
Cuando termine el bucle el subvector quedará organizado de la siguiente forma:

Se intercambia el pivote (posición ini) con el último de la
zona de los menores (posición lim-1) y con ello se termina la partición
del vector:
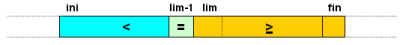
La nueva posición del pivote (el valor que se debe devolver) estará dada por
lim-1. La implementación del método sería la siguiente:
particion(vec: ARRAY[COMPARABLE]; ini,fin,pos_piv: INTEGER) : INTEGER is
-- Reorganiza los elementos del subvector vec[ini..fin] de manera que los
-- elementos menores que el pivote (el elemento en posicion pos_piv) esten
-- al inicio del vector, despues el elemento pivote (cuya posicion se devuelve)
-- y por ultimo los elementos mayores o iguales que el pivote.
local
i,lim : INTEGER;
do
vec.swap(ini,pos_piv);
from
i := ini+1;
lim := ini+1;
until i > fin loop
if vec.item(i) < vec.item(ini) then
vec.swap(i,lim);
lim := lim+1
end
i := i+1
end
vec.swap(ini,lim-1);
Result := lim-1
end -- particion
Voy a reescribir los métodos de las dos preguntas anteriores (búsqueda y ordenación) utilizando
precondiciones, postcondiciones e invariantes.
El método busqueda tiene como precondición que el vector esté ordenado, y
como postcondición que el resultado sea un indice que cumpla que el elemento apuntado (si existe) sea
mayor o igual, y el elemento anterior (si existe) sea menor. Por otra parte, se debe comprobar que durante
la ejecución del bucle los valores de izda y dcha sean adecuados (ver la
discusión del algoritmo). Tambien es necesario que el valor del punto medio esté
dentro del rango y que al finalizar el bucle izda y dcha esten en posiciones
contiguas:
busqueda(vec: ARRAY[COMPARABLE]; val: COMPARABLE): INTEGER is
-- Devuelve la menor posición del vector que contiene un valor igual o mayor que val.
-- Si todos los elementos son menores que val o el vector está vacío
-- devuelve la posición siguiente a la última del vector.
-- Eficiencia: O(lg n) sin precondiciones, O(n) con precondiciones.
require
vector_ordenado: esta_ordenado(vec);
local
izda,dcha,med : INTEGER;
do
from
izda := vec.lower;
dcha := vec.upper;
invariant
descarte_izdo: izda > vec.lower implies vec.item(izda-1) < val;
descarte_dcho: dcha < vec.upper implies vec.item(dcha+1) >= val;
variant
region_decreciente: dcha-izda+1
until izda > dcha loop
med := (izda+dcha)//2;
check medio_en_rango: izda <= med and med <= dcha end;
if vec.item(med) < val then
izda := med+1
else
dcha := med-1
end
end
check solapamiento_correcto: izda = dcha+1 end
Result := izda
ensure
rango_correcto: vec.lower <= Result and Result <= vec.upper+1;
region_ant_menor: Result > vec.lower implies vec.item(Result-1) < val;
region_sig_mayor: Result <= vec.upper implies vec.item(Result) >= val;
end -- busqueda
Se debe definir un método adicional para comprobar la precondición (vector ordenado):
esta_ordenado(vec: ARRAY[COMPARABLE]) : BOOLEAN is
local
i : INTEGER;
do
from i := vec.lower+1
until i > vec.upper or else vec.item(i-1) > vec.item(i) loop
i := i+1
end
Result := i > vec.upper
end -- ordenado
El método ordenar principal no tiene precondiciones (no exige ningún requisito al
vector). Sus postcondiciones deben garantizar que realiza su tarea (ordena el vector):
ordenar(vec: ARRAY[COMPARABLE]) is
-- Ordena el vector vec de menor a mayor por el algoritmo quicksort
do
if vec.count > 1 then
quicksort(vec,vec.lower,vec.upper)
end
ensure
vector_ordenado: esta_ordenado(vec);
-- No es necesario comprobar que contiene los mismos elementos
-- que el vector original porque todas las modificaciones se
-- realizan mediante intercambios (metodo swap).
end -- ordenar
El método quicksort tiene como precondición que el vector
no esté vacío. Como postcondición se debería comprobar que
lleva a cabo su tarea (ordena la parte del vector entre los índices ini
y fin), pero no se hace porque ya se lleva a cabo la comprobación en
el método ordenar y al ser un método recursivo el comprobar
la postcondición reduciría demasiado la eficiencia.
quicksort(vec: ARRAY[COMPARABLE]; ini,fin: INTEGER) is
-- Ordena el subvector vec[ini..fin] de menor a mayor.
require
rango_correcto : ini >= vec.lower and fin <= vec.upper
subvector_no_vacio : ini <= fin
local
pos_piv : INTEGER;
do
-- Se realiza una particion del subvector tomando como pivote
-- el elemento que se encuentra en la mitad
pos_piv := particion(vec,ini,fin,(ini+fin) // 2);
-- Se ordena recursivamente la zona de menores o iguales al pivote
if pos_piv > ini then quicksort(vec,ini,pos_piv-1) end
-- Se ordena recursivamente la zona de mayores o iguales al pivote
if pos_piv < fin then quicksort(vec,pos_piv+1,fin) end
ensure
-- Subvector vec[ini..fin] contiene los mismos elementos y está ordenado
-- No se producen cambios fuera del subvector vec[ini..fin]
end -- quicksort
El método particion tiene como precondiciones que los
parámetros ini, fin, pos_piv tengan sentido, y como postcondición
que particione adecuadamente el vector y devuelva la nueva posición del pivote. En el
bucle se va a incluir como invariante que la zona recorrida tenga la distribución
adecuada (ver pregunta anterior para comprender el algoritmo de partición).
particion(vec: ARRAY[COMPARABLE]; ini,fin,pos_piv: INTEGER) : INTEGER is
-- Reorganiza los elementos del subvector vec[ini..fin] de manera que los
-- elementos menores que el pivote (el elemento en posicion pos_piv) esten
-- al inicio del vector, despues el elemento pivote (cuya posicion se devuelve)
-- y por ultimo los elementos mayores o iguales que el pivote.
require
rango_correcto : ini >= vec.lower and fin <= vec.upper
subvector_no_vacio : ini <= fin
pivote_en_subvector : (ini <= pos_piv) and (pos_piv <= fin)
local
i,lim : INTEGER;
do
-- Se mueve el pivote al principio
vec.swap(ini,pos_piv);
-- Se recorren el resto de posiciones del vector, manteniendo en todo
-- momento la siguiente estructura: Los elementos menores que el pivote
-- se encuentran en las posiciones ini+1..lim-1 y los elementos mayores
-- o iguales en las posiciones lim..i-1
from
i := ini+1;
lim := ini+1;
invariant
limite_correcto_1 : lim > ini+1 implies vec.item(lim-1) < vec.item(ini);
limite_correcto_2 : lim < i implies vec.item(lim) >= vec.item(ini);
variant
fin-i
until i > fin loop
if vec.item(i) < vec.item(ini) then
-- Se intercambia con el primero de la zona de mayores o iguales
-- de forma que pase a estar al final de la zona de menores
vec.swap(i,lim);
-- Se incrementa la zona de menores
lim := lim+1
end
i := i+1
end
-- Se mueve el pivote al limite de separacion entre menores y
-- mayores o iguales intercambiandolo con el ultimo de la
-- zona de menores
vec.swap(ini,lim-1);
-- Se devuelve la posicion del pivote
Result := lim-1
ensure
pivote_en_limites: ini <= Result and Result <= fin;
particion_correcta1: subvector_menor_igual(vec,ini,Result-1,Result);
particion_correcta2: subvector_mayor_igual(vec,Result+1,fin,Result);
end -- particion
Se definen métodos adicionales para comprobar si la partición es correcta:
subvector_menor_igual(vec: ARRAY[COMPARABLE]; ini,fin,pos: INTEGER) : BOOLEAN is
-- Devuelve true si todos los elementos del subvector vec[ini..fin] son
-- menores o iguales que el elemento de vec en la posicion pos.
require
rango_correcto : ini >= vec.lower and fin <= vec.upper
posicion_correcta : pos >= vec.lower and pos <= vec.upper
local
i : integer;
do
Result := true;
from i := ini until i > fin or not Result loop
if vec.item(i) > vec.item(pos) then Result := false end
i := i+1
end
end -- subvector_menor_igual
subvector_mayor_igual(vec: ARRAY[COMPARABLE]; ini,fin,pos: INTEGER) : BOOLEAN is
-- Devuelve true si todos los elementos del subvector vec[ini..fin] son
-- mayores o iguales que el elemento de vec en la posicion pos.
require
rango_correcto : ini >= vec.lower and fin <= vec.upper
posicion_correcta : pos >= vec.lower and pos <= vec.upper
local
i : integer;
do
Result := true;
from i := ini until i > fin or not Result loop
if vec.item(i) < vec.item(pos) then Result := false end
i := i+1
end
end -- subvector_mayor_igual
Si la aplicación funciona bien pero va muy lenta, podeis probar
a compilarla con la opción boost:
compile -boost nombre_aplicacion.e ...
Esta opción desactiva la comprobación de precondiciones y
postcondiciones (no sólo las que hayais escrito vosotros, también
las del código de todas las librerias, por ejemplo la comprobación
de acceso en rango a un array, etc). Vereis que la aplicación va más
rápida, aunque a costa de no poder detectar posibles errores.
Por eso este paso sólo se debe dar cuando esteis razonablemente seguros
de que la aplicación no contiene errores.
Si a pesar de ello va demasiado lenta, entonces debeis analizar cuales son las
operaciones que tardan demasiado (tipicamente la búsqueda y ordenación)
y cambiar los algoritmos (en esta página os proporciono ejemplos de algoritmos
eficientes para esas tareas).