| ||||||||||||||
El objetivo de la práctica será crear un programa en Pascal que resuelva ecuaciones lineales de primer orden que se ajusten a unas ciertas restricciones, siguiendo la metodología de tipos abstractos de datos para el diseño de las tipos de datos utilizados, y proporcionando cierta documentación asociada al programa (tabla de casos de prueba, operaciones de las estructuras de datos definidas, precondiciones y postcondiciones, órdenes asintóticos).
El programa leerá una cadena de caracteres que contiene la ecuación a resolver y mostrará su solución, en un determinado formato, o bien un mensaje de error si la entrada no se ajusta a las restricciones del problema. Las ecuaciones que puede resolver el programa se deben ajustar a las siguientes restricciones:
Si una ecuación cumple las condiciones anteriores, entonces siempre es posible resolverla obteniendo el valor que debe tener la variable x.
El comportamiento del programa será leer una linea de texto, sin mostrar ningún mensaje previo (se puede suponer que la linea no supera los 255 caracteres), procesarla y escribir el resultado por pantalla (ya sea la solución o un mensaje de error) tras lo cual termina su ejecución. Ya que parte de la evaluación de la práctica será automática, es importante que lo que escribe el programa en pantalla se ajuste exactamente a las especificaciones de la práctica (se deben evitar pantallas de presentación, mensajes del tipo "pulse intro para empezar", "¿desea repetir?", etc.)
III. Etapas para la resolución del problema
Aunque este problema se puede resolver de muchas formas distintas, en este caso se debe seguir exactamente el esquema que se detalla a continuación:
1. Traducción de la cadena de caracteres a una lista de términos
En esta etapa se traduce la cadena de caracteres leida a una lista de los términos que componen la ecuación. Los términos pueden ser de cinco tipos distintos: Operadores, paréntesis izquierdo, paréntesis derecho, la variable x y números reales. La traducción se realiza creando una lista vacía y recorriendo los caracteres de la cadena interpretándolos de manera adecuada y creando e insertando en la lista los datos que representen a cada término:
Ejemplos de traducción:
| 1.23 | + | 2.45 |
| 1 | + | 0.45 |
| 1.23 | x | + | * | x | 2.45 |
| - | 4 | * | ( | - | 5 | - | 2 | ) | / | ( | - | x | - | - | 3 | ) | = | - | 1 | / | - | 2 |
2. Resolución de ambiguedades entre el operador resta y la negación
Dentro de una expresión, el símbolo "-" puede representar tanto al operador resta como al operador negación. Para resolver esta ambiguedad es necesario tener en cuenta el contexto en que aparece. En la etapa anterior se ha supuesto que toda aparición de "-" representa el operador resta. En esta etapa se recorrerá la lista obtenida y por cada término que corresponda a un operador resta se realizarán las siguientes comprobaciones:
Ejemplo: Aplicando esta etapa a la lista obtenida en el último ejemplo de la etapa anterior, la lista pasaría a contener los siguientes términos:
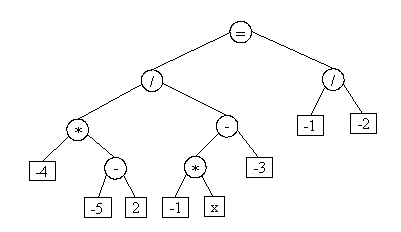
| -4 | * | ( | -5 | - | 2 | ) | / | ( | -1 | * | x | - | -3 | ) | = | -1 | / | -2 |
Nota: En esta etapa no se detectan errores en la ecuación.
3. Conversión de la expresión en un arbol binario
La forma más natural de representar una expresión matemática donde sólo intervengan operadores binarios es mediante un arbol donde las hojas almacenan números o variables y el resto de nodos almacenen operadores. En este último caso, los hijos izquierdo y derecho de los nodos son los operandos del operador almacenado en el nodo. En el ejemplo anterior, el arbol binario que representa esa ecuación sería:

Uno de los algoritmos que se pueden utilizar para convertir la lista en un arbol es representar la ecuación en notación postfija y evaluarla. Pulse aquí si desea obtener una información más detallada sobre este algoritmo.
En esta etapa se deben detectar los errores asociados a una expresión mal formada. En ese caso, el programa mostrará uno de los siguientes mensajes de error:
Nota: Si una expresión contiene varios errores, el programa debe mostrar sólo un mensaje de error, no todos los que aparezcan. Es decir, en el momento en que se detecta un error se muestra el mensaje asociado y no se hacen mas intentos para traducir la expresión ni para detectar otros errores.
4. Resolución de la ecuación
Resolver la ecuación es un proceso donde realizamos operaciones de reestructuración del arbol que representa a la ecuación, obteniendo por lo tanto nuevas ecuaciones, hasta obtener una ecuación de la forma x = expresión, es decir un arbol donde la raiz sea el operador igual y su hijo izquierdo la variable x.
Las operaciones de reestructuración se basan en aplicar las siguientes reglas aritméticas:
| a = f(x) | ==> | f(x) = a |
| f(x)+a = b | ==> | f(x) = b-a |
| f(x)-a = b | ==> | f(x) = b+a |
| a-f(x) = b | ==> | f(x) = a-b |
| f(x)*a = b | ==> | f(x) = b/a |
| f(x)/a = b | ==> | f(x) = b*a |
| a/f(x) = b | ==> | f(x) = a/b |
Nota: En las ecuaciones anteriores, f(x) hace referencia a la parte de la expresión que contiene a la variable x, y a, b, a partes de la expresión donde no aparece x. El símbolo ==> significa se puede sustuir por.
Aplicando sucesivamente la regla que corresponda a la estructura actual del arbol, al final se obtendra una ecuación donde en la parte izquierda de la igualdad esté unicamente la variable x. En el ejemplo anterior, el arbol que se obtendría al final sería el siguiente:
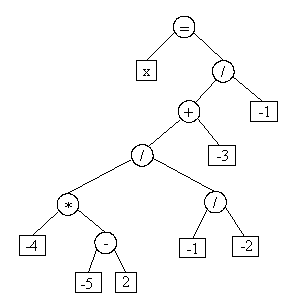
Al escribir este arbol por pantalla, el resultado sería:
x = ((((-4.00*(-5.00-2.00))/(-1.00/-2.00))+-3.00)/-1.00)
Debe notarse que la expresión debe escribirse completamente parentizada.
5. Evaluación de la expresión
La parte final corresponde a la evaluación de la expresión que queda a la derecha del operador igual.
La salida que debe mostrar el algoritmo es la ecuación asociada al arbol de la etapa 4 a la que sigue un símbolo igual y el valor resultante de la evaluación de la expresión. Los números de tipo real se escribirán con una precisión de dos decimales. Al contrario que en la lectura, se puede utilizar la sentencia write para escribir el valor. En el caso anterior, la salida sería:
x = ((((-4.00*(-5.00-2.00))/(-1.00/-2.00))+-3.00)/-1.00) = -53.00
IV. Documentación que se debe aportar
La práctica constará de una parte de código (el programa Pascal) y otra parte de documentación (impresa). El código estará constituido como mínimo por los siguientes ficheros (y con esos nombres):
Si se utiliza como método de conversión de expresiones en árboles binarios el paso a notación postfija, entonces se definiría la siguiente unidad:
Estas tres últimas unidades (UARBOL, ULISTA, UPILA) deben definir estructuras genéricas, es decir, que puedan almacenar elementos de cualquier tipo y no sólo los que se utilizan en este problema. Deben ser además estructuras dinámicas, que puedan almacenar un número ilimitado de elementos.
La documentación impresa consistirá en lo siguiente:
La codificación del programa debe seguir las normas de la programación estructurada, y eso implica, entre otras, las siguientes restricciones:
Por otra parte, para la realización de la práctica es necesario conocer algunas carácteristicas de Pascal que no se han contemplado en Programación I (se verán en Programación II):
VI. Presentación de la práctica
La práctica es individual y voluntaria, y supone un 10% de la nota de la asignatura. La presentación será presencial, en un horario y lugar que se establecerá a posteriori, y consistirá en la entrega de la documentación impresa y la comprobación de que el código del programa resuelve correctamente el problema planteado.
Puede contactar por e-mail con el profesor de la asignatura en la dirección cvaca@infor.uva.es