Problema 12
12. Resolver el problema de las torres de Hanoi con tres postes cuando se parte de cualquier posición válida. Sugerencia: Encontrar primero un esbozo de solución y diseñar despues el tipo de datos que represente la posición de los discos que sea más adecuado para esa forma de resolver el problema. Evaluar el orden del algoritmo obtenido.
Para resolver este problema es necesario familiarizarse un poco con él. El siguiente programa permite indicar los movimientos necesarios para resolver el problema (pulsando en el poste de origen y luego en el poste de destino), o bien observar las etapas necesarias para su resolución mediante los dos algoritmos que se proponen, pulsando el botón Resolver y el botón inferior donde se indica cada etapa.
En primer lugar, numeraremos los discos desde 1 hasta n en función de su diametro. Suponiendo una disposición correcta, siempre tendremos que en cualquier poste debajo de un disco debe existir otro con un índice mayor. Por lo tanto, siempre existirá algún poste que contenga como disco superior el disco 1.
El algoritmo se basa en la observación de que, independientemente de donde estén situados los discos, siempre que exista una subtorre formada por los discos 1 a i, podemos moverla utilizando el algoritmo clásico a cualquier otro poste, ya que los discos restantes (i+1 .. n) no suponen un obstáculo.
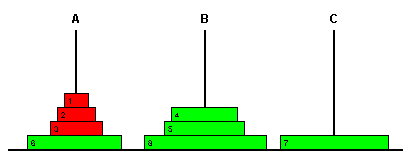
Por ejemplo, en la disposición que se muestra existe una subtorre en el poste A con los discos 1 a 3 (mostrados en rojo). Esta subtorre se puede mover a cualquier otro poste.

El disco i+1 (en este caso el disco 4) debe encontrarse en un poste distinto a éste (el A), ya que en caso contrario tendriamos una subtorre con los discos 1 a i+1. Además, debe ser el disco superior de su poste, ya que sólo puede estar encima suyo un disco menor (1..i), y todos los discos menores estan en la subtorre.
Por lo tanto, siempre es posible mover una subtorre con los discos 1..i al poste donde se encuentra el disco i+1. En este caso eso significa mover la subtorre 1..3 del poste A al poste B, lo que se puede hacer aplicando el algoritmo clásico con una llamada a HANOI3(3,'A','B','C'). El resultado sería el siguiente:
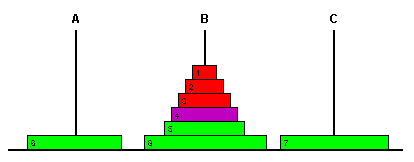
Ahora tenemos una subtorre con, como mínimo, un disco más (en este caso una subtorre 1..5) a la que podemos aplicar el mismo razonamiento. Como al principio, en el peor de los casos, tenemos una subtorre con el disco 1, basta con aplicar n veces este esquema para que terminemos con todos los discos agrupados en una subtorre 1..n. El último paso será aplicar el algoritmo clásico sobre esta subtorre para moverla al disco de destino (si no se encuentra ya en él).
Una posible codificación de este algoritmo sería la siguiente:
uses uHanoi;
...
procedure Hanoi3(var H: TTorresHanoi; N: integer; Orig,Dest,Aux: char);
{ Variante del algoritmo clásico donde además de escribir los movimientos
se adapta la información almacenada en H. }
begin
if n = 1 then
begin
writeln(output,Orig,' -> ',Dest);
Mover(H,Orig,Dest)
end else begin
Hanoi3(H,N-1,Orig,Aux,Dest);
writeln(output,Orig,' -> ',Dest);
Mover(H,Orig,Dest);
Hanoi3(H,N-1,Aux,Dest,Orig)
end
end;
function PosteRestante(Poste1,Poste2: char) : char;
{ Indica cual es el poste auxiliar (distinto de Poste1 y Poste2) }
begin
case Poste1 of
'A': if Poste2 = 'B' then PosteRestante := 'C' else PosteRestante := 'B';
'B': if Poste2 = 'A' then PosteRestante := 'C' else PosteRestante := 'A';
'C': if Poste2 = 'B' then PosteRestante := 'A' else PosteRestante := 'B';
end
end;
procedure HanoiGeneral(var H: TTorresHanoi);
{ Resuelve el problema de las torres de Hanoi comenzando con la disposicion de los discos
indicada en H y terminando con los discos situados en el ultimo poste }
var
Disco: integer;
PosteOrigen,PosteDestino : char;
begin
for Disco := 1 to NumDiscos(H)-1 do
begin
PosteOrigen := PosteDeDisco(H,1);
PosteDestino := PosteDeDisco(H,Disco+1);
if PosteOrigen <> PosteDestino then
Hanoi3(H,Disco,PosteOrigen,PosteDestino,PosteRestante(PosteOrigen,PosteDestino))
end;
{ Ya estan los discos agrupados. Ahora se mueven al último poste. }
PosteOrigen := PosteDeDisco(H,1);
if PosteOrigen <> 'C' then
Hanoi3(H,NumDiscos(H),PosteOrigen,'C',PosteRestante(PosteOrigen,'C'))
end;
Para realizar el código anterior se ha seguido un enfoque orientado a Tipos Abstractos de Datos: Se ha definido los tipos de datos que almacenan la información sobre el estado de las torres en función de las operaciones necesarias para éste problema concreto. Estas operaciones se muestran en azul en el código.
El tipo de datos concreto y la implementación de las operaciones se realizan en la unidad uHanoi:
unit uHanoi;
interface
const MaxDiscos = ...;
type
TTorresHanoi = ...;
{ Establece el número de discos del problema e inicializa las posiciones al valor
estándar (todos los discos en el poste A) }
procedure Inicializar(var H: TTorresHanoi; Num: integer);
{ Devuelve el número de discos del problema }
function NumDiscos(H: TTorresHanoi) : integer;
{ Devuelve el poste donde se encuentra el disco }
function PosteDeDisco(H: TTorresHanoi; Disco: integer) : char;
{ Adapta el estado de las torres de manera que el menor disco del poste origen pase a estar
en el poste destino, pasando a ser su menor disco (no se comprueba que el movimiento sea válido) }
procedure Mover(var H: TTorresHanoi; Origen,Destino: char) : integer;
implementation
...
end;
Ahora es necesario decidir cual es la estructura de datos más adecuada para representar la información del estado de las torres de Hanoi. El criterio será conseguir una implementación eficiente de las operaciones necesarias. A priori, existen varias posibilidades:
Se puede evaluar inmediatamente como se comportaría cada implementación con las operaciones definidas, teniendo en cuenta que la operación mover implica encontrar el menor disco de un poste dado, y hacer que pase a ser el menor disco de otro poste (se ha analizado por separado cada parte de la operación mover, en la tabla se muestra como una suma de ordenes):
| Lista de pares | Vector indexado por poste | Vector indexado por disco | Matriz poste/disco | |
|---|---|---|---|---|
| PosteDeDisco | O(n) | O(n) | O(1) | O(1) |
| Mover | O(n)+O(1) | O(1)+O(1) | O(n)+O(1) | O(n)+O(1) |
Las mejores implementaciones son el vector de listas indexado por poste y el vector indexado por disco (la matriz poste/disco ocupa mas espacio que las otras), aunque ninguna de las dos se comporta mejor que la otra para las dos operaciones. Para conseguir un orden O(1) en las dos operaciones se van a utilizar las dos implementaciones a la vez: Un vector, indexado por poste, almacena la lista ordenada de discos que contiene, y otro vector, indexado por disco, almacena el poste donde se encuentra cada disco.
Para representar las listas de discos del primer vector se ha elegido una implementacion contigua (arrays), debido a que las únicas operaciones a realizar sobre las listas son acceso, borrado e inserción del primer elemento.
unit uHanoi;
interface
const MaxDiscos = ...;
type
TTorresHanoi = record
{ VecTam almacena el tamaño (número de elementos) de cada lista de VecLis }
VecTam : array['A'..'C'] of integer;
{ VecLis almacena 3 listas, una por poste, donde se almacenan los discos (de mayor a
menor) que pertenecen a cada poste. Cada lista se representa por un array }
VecLis : array['A'..'C',1..MaxDiscos] of integer;
{ VecPos que almacena el poste donde se encuentra cada disco }
VecPos : array[1..MaxDiscos] of 'A'..'C'
end;
...
implementation
procedure Inicializar(var H: TTorresHanoi; Num: integer);
var Disco : integer;
begin
{ Todos los discos están en el poste A }
H.VecTam['A'] := Num;
H.VecTam['B'] := 0;
H.VecTam['C'] := 0;
for Disco := 1 to Num do
begin
{ Las listas almacenan los discos de mayor a menor }
H.VecLis['A',Num-Disco+1] := Disco;
H.VecPos[Disco] := 'A'
end
end;
function NumDiscos(H: TTorresHanoi) : integer;
begin
{ El numero total de discos será la suma de los discos de cada poste }
NumDiscos := H.VecTam['A']+H.VecTam['B']+H.VecTam['C']
end;
function PosteDeDisco(H: TTorresHanoi; Disco: integer) : char;
begin
PosteDeDisco := H.VecPos[Disco]
end;
procedure Mover(var H: TTorresHanoi; Origen,Destino: char);
var Disco : integer;
begin
{ El disco menor de Origen será el último de la lista de
los discos que pertenecen a ese poste }
Disco := H.VecLis[Origen,H.VecTam[Origen]];
{ El poste origen pasa a tener un disco menos }
H.VecTam[Origen] := H.VecTam[Origen]-1;
{ El poste destino pasa a tener un disco mas }
H.VecTam[Destino] := H.VecTam[Destino]+1;
{ Se inserta el disco al final de la lista de discos del poste destino }
H.VecLis[Destino,H.VecTam[Destino]] := Disco;
{ Por ultimo, se cambia el poste del disco en VecPos }
H.VecPos[Disco] := Destino
end;
end. { Unidad uHanoi }
Algoritmo mejorado
En general, es posible resolver el problema usando menos movimientos que el algoritmo anterior si nos damos cuenta de que además de poder mover la subtorre, siempre es posible mover un disco entre los otros postes distintos a los que contienen la subtorre. Es posible que el mover ese disco consigamos obtener una subtorre de mayor tamaño, con lo que ahorraríamos movimientos. Por ejemplo, en la siguiente situación:
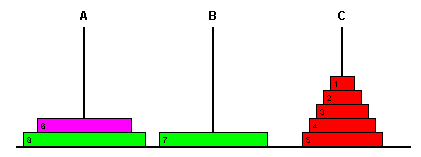
Si antes de mover la subtorre 1..5 movemos el disco 6 al poste B, obtenemos:
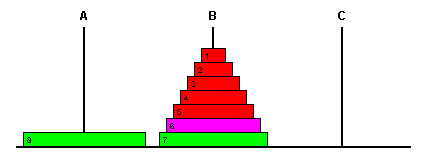
Ahora conseguimos una subtorre con los discos 1..7 en lugar de una subtorre con 1..6, evitando un movimiento de subtorre.
Regresar a la página de enunciados.